Table of Contents
Q-Learning是增强学习中model free的的重要算法,其基本思想是通过Q表记录并更新状态-行动的价值,使得最后获得一个“完美”的Q表:当agent处于任意状态时,查询该Q表即可获知如何行动。
下面通过一个非常简单的小例子来说明Q Learning的思想(本案例主要参考了: https://morvanzhou.github.io/tutorials/ )。这是一个来自一维世界的agent,它只能在一个固定长度的线段上左右运动,每次只能运动一格,当运动到线段的最右边时才会获得奖励:+1的reward。初始时,agent位于线段的最左边,它并不知道在线段的最右边有个“宝物”可以获得reward。
下面的一篇文章可以参考:https://blog.csdn.net/Young_Gy/article/details/73485518
import numpy as np
import pandas as pd
import time
定义系统参数
N_STATES = 6 # the length of the 1 dimensional world
ACTIONS = ['left', 'right'] # available actions
EPSILON = 0.9 # greedy police,这里的意思是,即便在Q表中有对应的(最佳)Q价值,也有10%的概率随机选取action
ALPHA = 0.1 # learning rate
GAMMA = 0.9 # discount factor
MAX_EPISODES = 7 # maximum episodes
FRESH_TIME = 0.01 # fresh time for one move
TERMINAL='bang' # 终止状态,当agent遇到最右边的宝物时设置此状态
DEBUG=True # 调试时设置为True则打印更多的信息
Q表的创建函数,初始化为0
本案例Q表的结构如下,其中最左边的一列是状态,本案例有6个状态,即agent可以在6个格子内左右移动:
| left | right | |
|---|---|---|
| 0 | 0 | 0 |
| 1 | 0 | 0 |
| 2 | 0 | 0 |
| 3 | 0 | 0 |
| 4 | 0 | 0 |
| 5 | 0 | 0 |
def build_q_table(n_states, actions):
table = pd.DataFrame(
np.zeros((n_states, len(actions))), # q_table initial values
columns=actions, # actions's name
)
print(table) # show table
return table
策略
这是增强学习中的策略部分,这里的策略很简单:如果平均随机采样值大于设定的epsilon或者当前状态的所有动作价值为0则随机游走探索(随机选取动作),否则从Q表选取价值最大的动作。我们的目标是不断优化Q表中的动作价值。
def choose_action(state, q_table):
# This is how to choose an action
state_actions = q_table.iloc[state, :]
# 如果当前状态的所有动作的价值为0,则随机选取动作
# 如果平均随机采样值 > EPSILON,则随机选取动作
if (np.random.uniform() > EPSILON) or ((state_actions == 0).all()):
action_name = np.random.choice(ACTIONS)
else: # act greedy
action_name = state_actions.idxmax()
return action_name
和环境的交互
环境接受agent的action并执行之,然后给出下一个状态和相应的reward。只有agent走到了最右边,环境才给予+1的reward,其他情况下reward=0。
def get_env_feedback(S, A):
# This is how agent will interact with the environment
# S_: next status
# R: reward to action A
if A == 'right': # move right
if S == N_STATES - 2: # terminate
S_ = TERMINAL
R = 1
else:
S_ = S + 1
R = 0
else: # move left
R = 0
if S == 0:
S_ = S # reach the wall
else:
S_ = S - 1
return S_, R
更新环境
这是agent和环境交互的一部分,绘制环境。
def update_env(S, episode, step_counter):
# This is how environment be updated
env_list = ['-']*(N_STATES-1) + ['T'] # '---------T' our environment
if S == TERMINAL:
interaction = 'Episode %s: total_steps = %s' % (episode+1, step_counter)
print('\r{}'.format(interaction), end='')
time.sleep(2)
print('\r ', end='')
else:
env_list[S] = 'o'
interaction = ''.join(env_list)
print('\r{}'.format(interaction), end='')
time.sleep(FRESH_TIME)
游戏的实现
rl = reinforcement learning
这里重点区分两个概念:
- q_predict,Q预测,即当前(S,A)在Q表中的值(简称Q价值),表达了在S状态下如果采取A动作的价值多少。这是在环境还没有接收并执行A动作时的Q价值,即此时A动作还没有真正执行,因此是一个预测值,或者说是上一轮(S,A)后的Q真实,如果存在上一轮的话。
- q_target,Q真实,即(S,A)执行后的Q价值:环境接收并执行了A动作,给出了S_(下一个动作)和R(reward),则根据Q Learning算法的更新公式可计算q_target。之所以叫做Q真实,是因为这个时候A动作已经被环境执行了,这是确凿发生的事实产生的Q价值。
画个图来进一步理解:
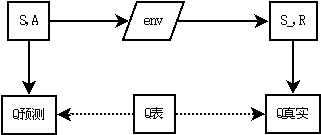
下图说明了Q Learning的算法(see: https://www.cse.unsw.edu.au/~cs9417ml/RL1/algorithms.html ):

def rl():
# main part of RL loop
q_table = build_q_table(N_STATES, ACTIONS)
for episode in range(MAX_EPISODES):
step_counter = 0
S = 0
is_terminated = False
update_env(S, episode, step_counter)
while not is_terminated:
A = choose_action(S, q_table)
# Q表中当前(S,A)对应的值称为Q预测,即当前的(S,A)组合的价值。
q_predict = q_table.loc[S, A]
S_, R = get_env_feedback(S, A) # take action & get next state and reward
if S_ != TERMINAL:
q_target = R + GAMMA * q_table.iloc[S_, :].max() # next state is not terminal
else:
q_target = R # next state is terminal
is_terminated = True # terminate this episode
q_table.loc[S, A] = q_predict + ALPHA * (q_target - q_predict) # update
if DEBUG == True and q_target != q_predict:
print(' %s episode,S(%s),A(%s),R(%.6f),S_(%s),q_p(%.6f),q_t(%.6f),q_tab[S,A](%.6f)' % (episode,S,A,R,S_,q_predict,q_target,q_table.loc[S,A]))
#print(q_table)
S = S_ # move to next state
update_env(S, episode, step_counter+1)
step_counter += 1
return q_table
执行强化学习训练
遗憾的是,还不知道在jupyter中如何不换行持续显示训练的过程,请高手指点。目前可以通过打开DEBUG开关观察agent的训练过程。
q_table = rl()
print('\r\nQ-table after training:\n')
print(q_table)
left right
0 0.0 0.0
1 0.0 0.0
2 0.0 0.0
3 0.0 0.0
4 0.0 0.0
5 0.0 0.0
----oT 0 episode,S(4),A(right),R(1.000000),S_(bang),q_p(0.000000),q_t(1.000000),q_tab[S,A](0.100000)
---o-T 1 episode,S(3),A(right),R(0.000000),S_(4),q_p(0.000000),q_t(0.090000),q_tab[S,A](0.009000)
----oT 1 episode,S(4),A(right),R(1.000000),S_(bang),q_p(0.100000),q_t(1.000000),q_tab[S,A](0.190000)
--o--T 2 episode,S(2),A(right),R(0.000000),S_(3),q_p(0.000000),q_t(0.008100),q_tab[S,A](0.000810)
---o-T 2 episode,S(3),A(right),R(0.000000),S_(4),q_p(0.009000),q_t(0.171000),q_tab[S,A](0.025200)
----oT 2 episode,S(4),A(right),R(1.000000),S_(bang),q_p(0.190000),q_t(1.000000),q_tab[S,A](0.271000)
-o---T 3 episode,S(1),A(right),R(0.000000),S_(2),q_p(0.000000),q_t(0.000729),q_tab[S,A](0.000073)
--o--T 3 episode,S(2),A(right),R(0.000000),S_(3),q_p(0.000810),q_t(0.022680),q_tab[S,A](0.002997)
---o-T 3 episode,S(3),A(right),R(0.000000),S_(4),q_p(0.025200),q_t(0.243900),q_tab[S,A](0.047070)
----oT 3 episode,S(4),A(right),R(1.000000),S_(bang),q_p(0.271000),q_t(1.000000),q_tab[S,A](0.343900)
o----T 4 episode,S(0),A(right),R(0.000000),S_(1),q_p(0.000000),q_t(0.000066),q_tab[S,A](0.000007)
-o---T 4 episode,S(1),A(right),R(0.000000),S_(2),q_p(0.000073),q_t(0.002697),q_tab[S,A](0.000335)
--o--T 4 episode,S(2),A(right),R(0.000000),S_(3),q_p(0.002997),q_t(0.042363),q_tab[S,A](0.006934)
---o-T 4 episode,S(3),A(right),R(0.000000),S_(4),q_p(0.047070),q_t(0.309510),q_tab[S,A](0.073314)
----oT 4 episode,S(4),A(right),R(1.000000),S_(bang),q_p(0.343900),q_t(1.000000),q_tab[S,A](0.409510)
o----T 5 episode,S(0),A(right),R(0.000000),S_(1),q_p(0.000007),q_t(0.000302),q_tab[S,A](0.000036)
-o---T 5 episode,S(1),A(right),R(0.000000),S_(2),q_p(0.000335),q_t(0.006240),q_tab[S,A](0.000926)
--o--T 5 episode,S(2),A(right),R(0.000000),S_(3),q_p(0.006934),q_t(0.065983),q_tab[S,A](0.012839)
---o-T 5 episode,S(3),A(right),R(0.000000),S_(4),q_p(0.073314),q_t(0.368559),q_tab[S,A](0.102839)
----oT 5 episode,S(4),A(right),R(1.000000),S_(bang),q_p(0.409510),q_t(1.000000),q_tab[S,A](0.468559)
o----T 6 episode,S(0),A(right),R(0.000000),S_(1),q_p(0.000036),q_t(0.000833),q_tab[S,A](0.000116)
-o---T 6 episode,S(1),A(right),R(0.000000),S_(2),q_p(0.000926),q_t(0.011555),q_tab[S,A](0.001989)
--o--T 6 episode,S(2),A(right),R(0.000000),S_(3),q_p(0.012839),q_t(0.092555),q_tab[S,A](0.020810)
---o-T 6 episode,S(3),A(right),R(0.000000),S_(4),q_p(0.102839),q_t(0.421703),q_tab[S,A](0.134725)
----oT 6 episode,S(4),A(right),R(1.000000),S_(bang),q_p(0.468559),q_t(1.000000),q_tab[S,A](0.521703)
Q-table after training:
left right
0 0.0 0.000116
1 0.0 0.001989
2 0.0 0.020810
3 0.0 0.134725
4 0.0 0.521703
5 0.0 0.000000
