强化学习的基本环境和流程
《Reinforcement learning, An Introduction》学习系列笔记。
强化学习中的MDP是Agent和Environment交互的过程,如下图所示:
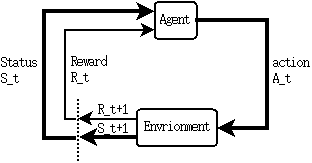
假设Agent的初始状态为\(S_0\),Agent根据自身的策略(随机或者某种特定的策略)采取了动作\(A_0\),Envrionment根据此动作给出了Agent的下一状态\(S_1\)和相应的Reward:\(R_1\),Agent再根据\(S_1\)决定采取动作\(A_1\),于是形成了如下的序列:
\[S_0,A_0,R_1,S_1,A_1,R_2,S_2,A_2,...\]也就是说,<S,A,R>三元组构成了MDP的主要过程。
dynamics funtion
dynamics function是MDP问题的一个基础函数: \(p(s',r\mid s,a)=P_r(S_t=s',R_t=r \mid A_{t-1}=a, S_{t-1}=s)\)
并且: \(\sum_{s'\in \mathcal{S}}\sum_{r\in \mathcal{R}} p(s',r\mid s,a)=1, \forall s\in\mathcal{S},\forall a\in\mathcal{A}(s)\)
dynamics function是一个四元概率函数,是对Environment的建模,即将Agent看做一个白盒(合理的假设,因为Agent对我们而言是完全可控的),则Agent的输入s和输出a对于Environment而言可以看做是Environment的输入,因此dynamics function的意义为:给定状态s和动作a,Environment输出下一时刻的状态s’及其相应的reward r的概率。
在MDP中,状态转移矩阵是一个重要的概念。有了dynamics function,状态转移矩阵可以表示为(传统的状态转移矩阵为\(\mathcal{p}_{s's}\),这里加入了a):
\[p(s'\mid s,a) = \sum_{r\in\mathcal{R}} p(s',r\mid s,a)\]对于reward的期望,即给定a,s时随机变量\(R_t\)的期望表示为:
\[r(s,a)=\mathbb{E}[R_t\mid S_{t-1}=s, A_{t-1}=a]=\sum_{r\in\mathcal{R}}r\sum_{s'\in\mathcal{S}}p(s',r\mid s,a)\]上式也可以表示为: \(r(s,a)=\mathbb{E}[R_t\mid S_{t-1}=s, A_{t-1}=a]=\sum_{r\in\mathcal{R}}\sum_{s'\in\mathcal{S}}rp(s',r\mid s,a)\)
也就是说,把r放到里面结果是一样的。但是,第一种表示方法更加直观的表达出了期望的计算方式。
\(r(s,a,s')\)则是一个表示即时奖励的标量函数,即Agent根据当前状态s做出动作a之后,环境在反馈一个s’的同时,也会反馈一个相应的reward。
对于三元组<s,a,s’>的reward期望,可以表示为: \(r(s,a,s')=\mathbb{E}[R_t\mid S_{t-1}=t,A_{t-1}=a,S_t=s'] \\=\sum_{r}r p(r\mid s,a,s') =\sum_{r}r\frac{p(r,s',s,a)}{p(s',s,a)}\)
由条件概率的定义可得:
\[p(s',r\mid s,a)=\frac{p(s',s,a,s')}{p(s,a)} \\p(s'\mid s,a)=\frac{p(s',a,s)}{p(s,a)}\]于是:
\[r(s,a,s')=\sum_{r}r\frac{p(s',r\mid s,a)}{p(s'\mid s,a)}\]画个图可以更直观的理解r(s,a,s’)的计算方法:
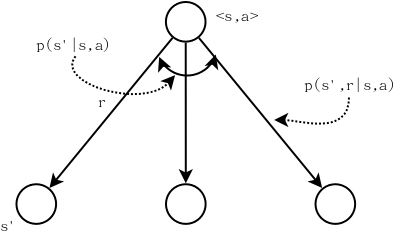
| 从图中可以看出$$\sum\frac{p(s’,r | s,a)}{p(s’ | s,a)} = 1$$。 |
案例分析
假设办公室有一个可充电的罐罐收集机器人,负责收集办公室的空的瓶瓶罐罐。这个机器人的充电状态为S{high, low},在电池电量为high时,机器人的动作空间为A{high}={search,wait},search表示四处游走寻找瓶瓶罐罐一个固定的时间(不会耗光电量),其reward为\(r_{search}\);wait表示原地等待有人送来一个罐罐,其reward为\(r_{wait}\),此时也不会耗光电量。显然,电池电量为high时去充电是愚蠢的行为,因此当电池电量为high时,其动作空间不包括recharge这个动作。当充电状态为low时,机器人的动作空间为A{low}={search, wait, recharge},其中search、wait的含义等同与电池电量高时的清醒,recharge的reward为0。但是,此时如果 执行search动作,可能会导致机器人耗光电量,机器人只能原地等待救援,我们假设其reward为-3。
假设电池电量高时research完成后电量仍然高的概率为\(\alpha\),电池电量低时research动作完成后电量依然低的概率为\(\beta\),于是本案例可表示为下图,其中无背景圆圈表示机器人的电池电量状态空间,黑色圆点表示机器人的动作空间。弧线上标注的是动作的概率及其reward值。可以看出,每一个动作的总的概率和为1。这是一个Agent视角的状态图。
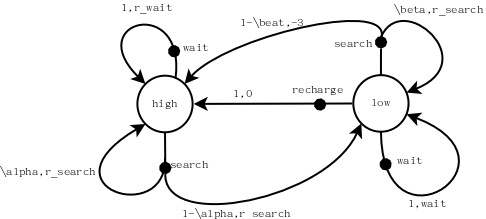
通过概率转移矩阵的方式描述本案例:
| s | a | s’ | \(r(s,a,s')\) | \(p(s'\mid s,a)\) | \(p(s',r\mid s,a)\) |
|---|---|---|---|---|---|
| high | search | high | \(r_{resarch}\) | \(\alpha\) | \(\alpha\) |
| high | search | low | \(r_{resarch}\) | \(1-\alpha\) | \(1-\alpha\) |
| high | wait | high | \(r_{wait}\) | 1 | 1 |
| high | wait | low | – | 0 | 0 |
| low | search | high | -3 | \(1-\beta\) | \(1-\beta\) |
| low | search | low | \(r_{resarch}\) | \(\beta\) | \(\beta\) |
| low | wait | high | – | 0 | 0 |
| low | wait | low | \(r_{wait}\) | 1 | 1 |
| low | recharge | high | 0 | 1 | 1 |
| low | recharge | low | – | 0 | 0 |
上表中,\(p(s'\mid s,a)=\sum_{r} p(s',r \mid s,a)\),但是由于<s,a,s’,r>是一一对应关系,因此\(p(s'\mid s,a)=p(s',r\mid s,a)\)
本案例重点是要学到使用MDP进行分析的基本步骤:
- 辨识Agent和Enviroment。
- 辨识Agent的状态空间\(\mathcal{S}\)
- 根据状态空间确定Agent的动作空间\(\mathcal{A}(\mathcal{S})\)
-
测量状态转移函数p(s’ s,a)或者p(s’,r s,a)
