策略评估的概念
策略评估(policy evaluation)是动态规划(dynamic programming)的一个基础性问题,即如何评估给定的策略\(\pi\)?我们已经知道最优策略(optimal policy)的定义为如果一个策略\(\pi\)使得\(v_{\pi}(s)\ge v_{\pi^{'}}(s),\forall s\in\mathcal{S}\),则称策略\(\pi\)优于策略\(\pi^{'}\)。因此,在策略评估中,如何求出\(v_{\pi}(s)\)就非常关键。
根据MDP值函数的贝尔曼公式,我们可以精确求解\(v_{\pi}(s)\):
\[v_{\pi}(s)=\sum_{a\in\mathcal{A}}\pi(a\mid s)\left(R_s^a+\gamma\sum_{s'\in\mathcal{S}}\mathcal{p}_{ss'}^a v_{\pi}(s')\right)\tag{1}\]贝尔曼公式无疑是完美的,漂亮的,表达了当前状态\(s\)和下一状态\(s'\)的递推关系。但是高维度的贝尔曼公式也是乏味的,求解困难的。怎么办呢?简单的循环迭代是计算机最擅长的事情了。如果我们构造一个价值函数的向量序列\(v_0,v_1,v_2,\ldots\)(这是理解价值函数迭代公式的关键所在),其中\(v_1\)是将\(v_0\)代入公式1所得,\(v_2\)是将\(v_1\)代入公式1所得,即\(v_0\)是第一次迭代的状态值函数向量,\(v_1\)是第二次迭代的状态值函数向量,以此类推,即有(这里偷换了向量和标量的概念,不影响理解和表达):
\[v_{k+1}(s)=\sum_{a\in\mathcal{A}}\pi(a\mid s)\left(R^a_{s}+\gamma\sum_{s'\in\mathcal{S}}\mathcal{P}_{ss'}^av_{k}(s')\right)\tag{2}\]式2即为计算价值函数的迭代公式,其中的k为迭代的步数。
这样,如果我们初始化\(v_0\)为向量\(0\)(这是最常见的假设),则根据式2即可逐步求得\(v_1,v_2,\ldots\),即逐步逼近\(v_{\pi}\)(可以证明,还没有看到这部分)。
理解式2的关键是,贝尔曼公式(式1)只是在空间上描述了状态间的关系,而式2更丰富,在空间和时间两个维度上描述了状态(值函数)之间的关系,即在时间维度上,\(v_{k+1}(s)\)是建立在\(v_{k}(s')\)的基础之上的,通俗的讲就是向量\(v_1\)是通过\(v_0\)计算出来的;在空间维度上,具体描述了两个值函数的结构关系,如下图所示:
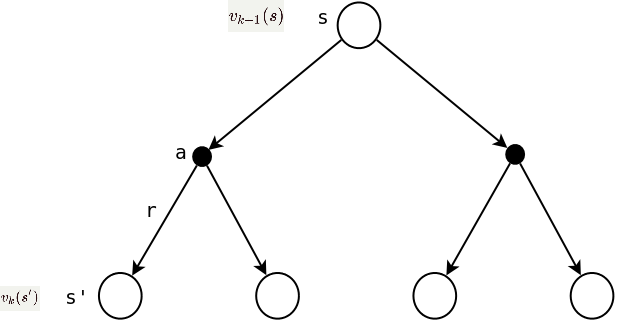
策略评估迭代公式的向量表达方式为:
\[\mathcal{v_{k+1}}=\mathcal{R}+\gamma\mathcal{P}\mathcal{v_k}\]策略评估案例分析:小小方格世界
如下图在4x4方格中,共有15种状态,其中灰色底色的方块表示终止状态(注意,此时图中的数字表示方块的序号,不是状态的价值)。游戏的规则是:
- agent在任意一个方块中共有4种动作{up,down,left,right};
- 每移动一步的即时奖励为-1;显然,在终止状态的奖励为0。
- 如果动作导致agent超出了边界,则agent回到移动前的状态;
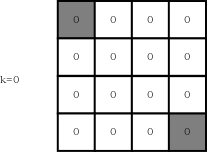
下面,我们评估一下随机游走的策略,即agent在一个状态下采取4种动作的概率均为0.25。首先,初始化所有的状态值函数为0(k=0),如下图所示:
如何计算下一轮迭代的状态值函数呢?以1号状态为例,画出1号状态的backup diagram如下图所示:
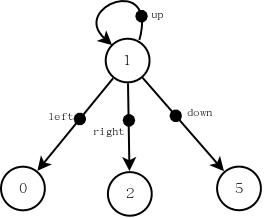
由此可以计算出1号状态的价值函数为:
\[v_1(1)=0.25\times q(1,up)+0.25\times q(1,down)+0.25\times q(1,left)+0.25\times q(1,right)\]式中,\(q(1,up)\)表示在状态1采取动作up的动作价值函数。以计算\(q(1,up)\)为例:
\[q(1,up)=-1+1\times 0=-1\]其中,-1是采取动作up的即时奖励;1是采取动作up时后续状态的转移概率。因为采取动作up后只有一个后续状态(超出边界回到状态1),因此转移概率为1;0是上一轮迭代时后续状态(这里依然是状态1)的值价值函数。
下面是计算1号状态价值函数在第一轮迭代(k=1)的完整过程:
\[\begin{align} v_1(1)=& 0.25\times(-1+1\times 0)+\tag{4-1,up}\\ & 0.25\times(-1+1\times0)+\tag{4-2,down}\\ & 0.25\times(-1+1\times0)+\tag{4-3,left}\\ & 0.25\times(-1+1\times0)\tag{4-4,right}\\ =-1 \end{align}\]很容易看出,在第一轮迭代结束时,除终止状态外,其他所有状态的价值函数均为-1,如下图所示(k=1):
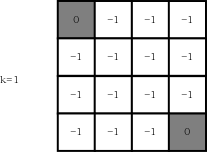
下面进行第二轮迭代,还是以状态1为例:
\[\begin{align} v_2(1)=& 0.25\times(-1+1\times -1)+ \tag{4-1,up} \\ & 0.25\times(-1+1\times-1)+ \tag{4-2,down}\\ & 0.25\times(-1+1\times0)+\tag{4-3,left}\\ & 0.25\times(-1+1\times-1)\tag{4-4,right}\\ =1.75 \end{align}\]第二轮迭代结束时,状态如下图所示(k=2):
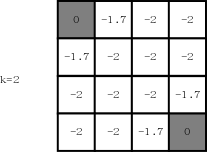
可以看出,离终止状态较近的状态其值函数更大一些,表示从这些状态到终止状态所需的步数更少。
后面轮次的计算过程不再赘述,下面分别是第三轮迭代后的状态(k=3):
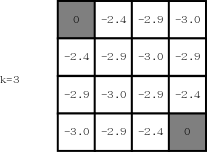
第十轮迭代后的状态(k=10):
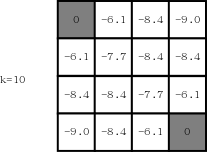
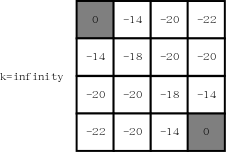
当\(k=\infty\)时,状态为: