蒙特卡罗方法
初识蒙特卡罗方法,是近似计算\(\pi\),觉得很神奇,如此简洁的思路,居然能干这么复杂的事。在解决MDP问题时,蒙特卡罗方法又一次显神威。
在model-free的环境中,如何评估状态的价值?我们无法知道环境内部的状态转移矩阵,此时蒙特卡罗方法就派上了用场。其实对于model-based的环境,也是可以使用蒙特卡罗方法的。
蒙特卡罗方法的基本出发点是,在给定的策略下,从任意状态s出发,我们可以获得一个episode,记这个episode的Return平均值为状态s的价值。只要满足以下两个条件,episode的Return平均值就会逼近状态s的价值:
- 足够多的episode
- 必须遍历所有的状态
注意这里的episode的含义:
- 显然,每个episode可能是实际采集的数据(历史经验值),也可以是自动产生的数据(模拟数据)。
- episode的长度不定。
- 在一个episode中,可能多次经过状态s,存在两种不同的蒙特卡罗算法:first-visit MC和every-visit MC。
蒙特卡罗算法的表述如下:

注意到,这里只涉及到状态的价值评估,即在给定的策略下评估各状态的价值(即策略的评估),不涉及到策略的优化。当然,策略评估是策略优化的基础。
21点游戏的蒙特卡罗价值评估
这里是简化版的21点游戏规则:开局时庄家(dealer)发两张牌,一明一暗。玩家(player)根据庄家的明牌、手中的总点数以及是否有ace(A)决定是否继续要牌(hit)。如果玩家停牌(stick),则庄家要翻开暗牌。此时如果庄家的总点数小于17点,则庄家要摸牌直到点数大于17点为止,然后计算玩家和庄家的点数,谁更逼近21点则胜出。
假设我们采用如下的策略:如果玩家的总点数小于20则继续要牌。注意,这里不是讨论策略优化问题,给定的这个策略也不是最优策略,我们在这里是使用蒙特卡罗方法来评估这个策略。
首先看一下21点游戏的状态空间。由于ace的特殊性,玩家会根据手中是否持有ace以及手中牌的总点数和庄家的明牌来决定下一步是否继续要牌,因此每一个状态是一个三元组(玩家手牌的总点数,庄家的明牌点数,玩家是否持有ace),分开来说:
- 玩家手牌的总点数:显然,玩家手中的牌的总点数如果小于12点则只能有一个动作选择:继续要牌(hit),这种总点数小于12点的状态对于建模和分析是没有意义的,因此要求模型的初始状态中,玩家手中的总点数要不小于12点,即玩家手牌的总点数的范围是[12,21],即玩家手牌的总点数有10种可能性。
- 庄家的明牌点数:如果此时庄家持有一个ace明牌,则这张ace显然庄家会按照1计算,否则玩家就太容易玩死庄家了:庄家bust的概率太高了。即,庄家明牌点数有10种可能性(ace记为1)。
- 玩家是否持有ace:如果玩家持有ace,则玩家可以根据当前手牌的总点数决定ace应该取1还是11使得手中总点数尽量大且不超过21点。
于是很可以看出,21游戏的总的状态空间为:\(10\times10\times2=200\)个状态。
下面针对这200个状态进行价值计算,即策略评估。下面是该策略的评估结果:
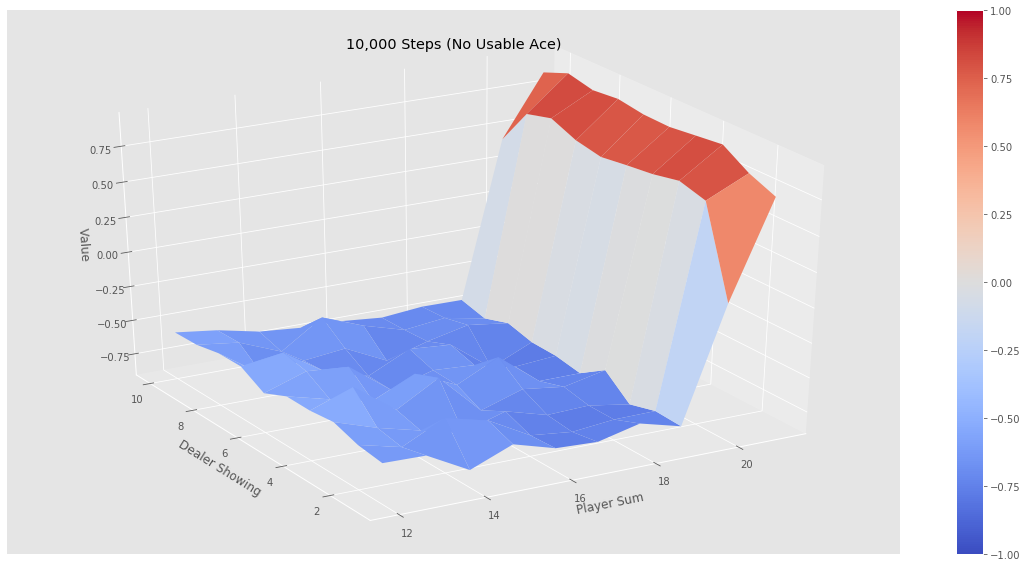
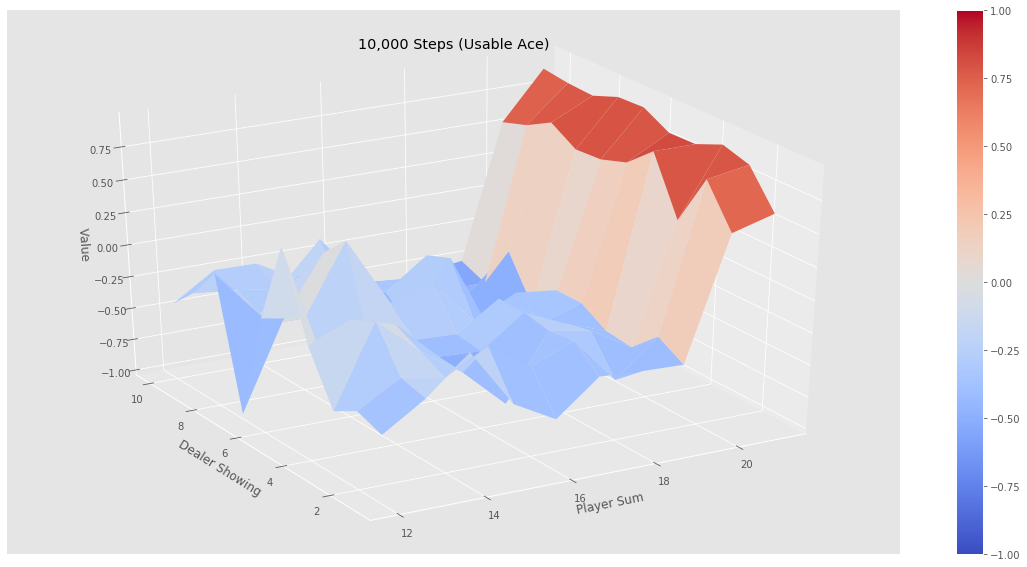
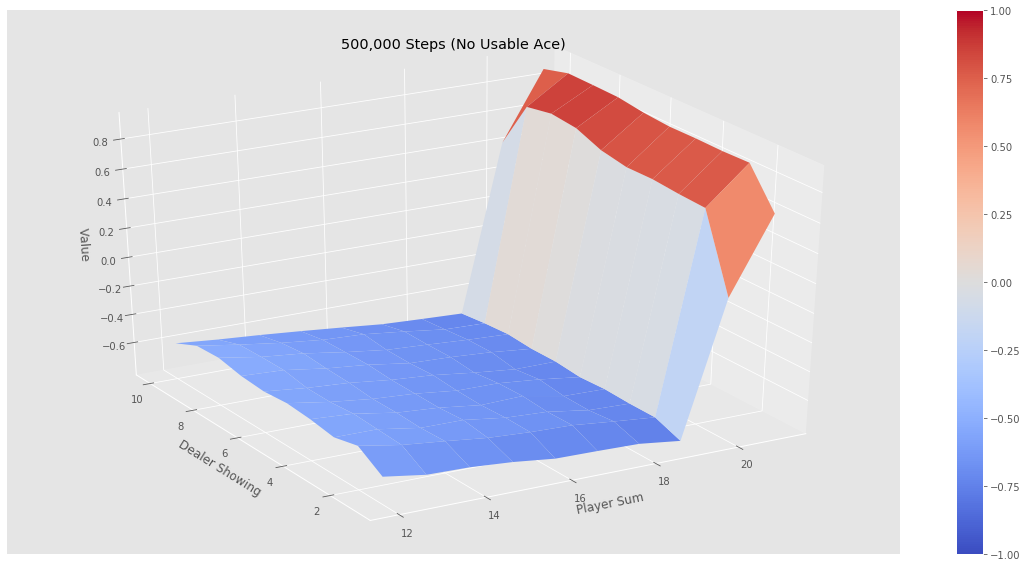
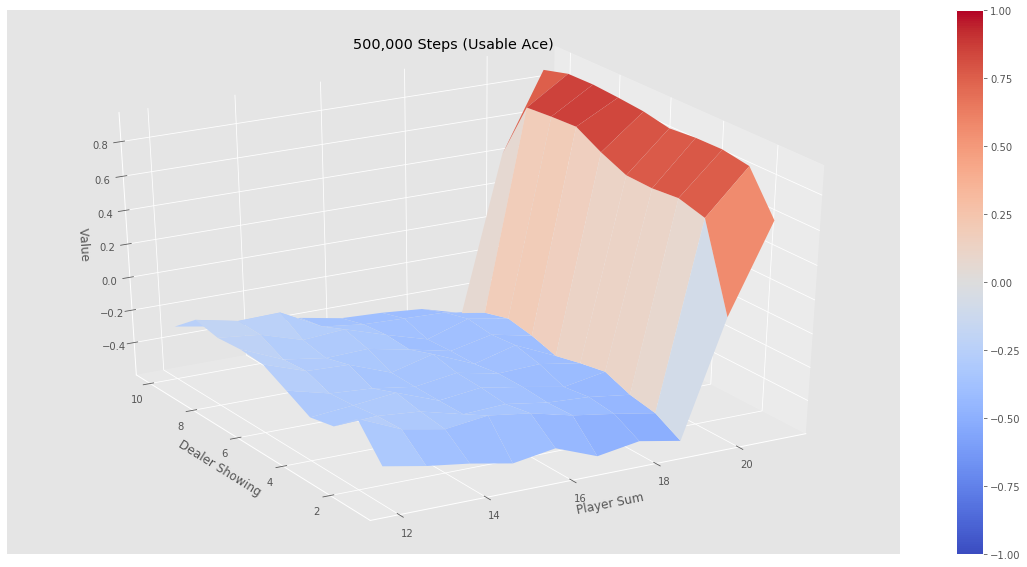
可以看出,在目前这个策略下,如果玩家的点数小于20是相当不利的,赢的概率断崖式下降,原因也很简单:玩家在点数接近20时继续要牌,爆掉的概率显然会大大增加。也就是说,这绝对不是一个好的策略。
gym环境和21点游戏的蒙特卡罗方法策略评估实现
感谢Denny Britz的工作,让我们可以轻松的直观感受蒙特卡罗方法的魅力(这里根据Denny Britz的代码略有改动)。分两步走:
gym环境的创建
这里采用了标准的gym接口实现了BlackjackEnv环境,代码如下:
import gym
from gym import spaces
from gym.utils import seeding
def cmp(a, b):
return int((a > b)) - int((a < b))
# 1 = Ace, 2-10 = Number cards, Jack/Queen/King = 10
deck = [1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 10, 10, 10]
def draw_card(np_random):
return np_random.choice(deck)
def draw_hand(np_random):
return [draw_card(np_random), draw_card(np_random)]
def usable_ace(hand): # Does this hand have a usable ace?
return 1 in hand and sum(hand) + 10 <= 21
def sum_hand(hand): # Return current hand total
if usable_ace(hand):
return sum(hand) + 10
return sum(hand)
def is_bust(hand): # Is this hand a bust?
return sum_hand(hand) > 21
def score(hand): # What is the score of this hand (0 if bust)
return 0 if is_bust(hand) else sum_hand(hand)
def is_natural(hand): # Is this hand a natural blackjack?
return sorted(hand) == [1, 10]
class BlackjackEnv(gym.Env):
"""Simple blackjack environment
Blackjack is a card game where the goal is to obtain cards that sum to as
near as possible to 21 without going over. They're playing against a fixed
dealer.
Face cards (Jack, Queen, King) have point value 10.
Aces can either count as 11 or 1, and it's called 'usable' at 11.
This game is placed with an infinite deck (or with replacement).
The game starts with each (player and dealer) having one face up and one
face down card.
The player can request additional cards (hit=1) until they decide to stop
(stick=0) or exceed 21 (bust).
After the player sticks, the dealer reveals their facedown card, and draws
until their sum is 17 or greater. If the dealer goes bust the player wins.
If neither player nor dealer busts, the outcome (win, lose, draw) is
decided by whose sum is closer to 21. The reward for winning is +1,
drawing is 0, and losing is -1.
The observation of a 3-tuple of: the players current sum,
the dealer's one showing card (1-10 where 1 is ace),
and whether or not the player holds a usable ace (0 or 1).
This environment corresponds to the version of the blackjack problem
described in Example 5.1 in Reinforcement Learning: An Introduction
by Sutton and Barto (1998).
https://webdocs.cs.ualberta.ca/~sutton/book/the-book.html
"""
def __init__(self, natural=False):
self.action_space = spaces.Discrete(2)
self.observation_space = spaces.Tuple((
spaces.Discrete(32),
spaces.Discrete(11),
spaces.Discrete(2)))
self._seed()
# Flag to payout 1.5 on a "natural" blackjack win, like casino rules
# Ref: http://www.bicyclecards.com/how-to-play/blackjack/
self.natural = natural
# Start the first game
self._reset() # Number of
self.nA = 2
def reset(self):
return self._reset()
def step(self, action):
return self._step(action)
def _seed(self, seed=None):
self.np_random, seed = seeding.np_random(seed)
return [seed]
def _step(self, action):
assert self.action_space.contains(action)
if action: # hit: add a card to players hand and return
self.player.append(draw_card(self.np_random))
if is_bust(self.player):
done = True
reward = -1
else:
done = False
reward = 0
else: # stick: play out the dealers hand, and score
done = True
while sum_hand(self.dealer) < 17:
self.dealer.append(draw_card(self.np_random))
reward = cmp(score(self.player), score(self.dealer))
if self.natural and is_natural(self.player) and reward == 1:
reward = 1.5
return self._get_obs(), reward, done, {}
def _get_obs(self):
return (sum_hand(self.player), self.dealer[0], usable_ace(self.player))
def _reset(self):
self.dealer = draw_hand(self.np_random)
self.player = draw_hand(self.np_random)
# Auto-draw another card if the score is less than 12
while sum_hand(self.player) < 12:
self.player.append(draw_card(self.np_random))
return self._get_obs()
蒙特卡罗方法进行策略评估
测试代码是jupyter格式的,不再赘述,可参考:MC prediction solution,我在其中根据自己的理解加了一些注释。
需要说明的是,如果没有在Denny Britz的源代码结构中运行上面的评估代码,需要略微调整一下代码最前面的import语句。
python知识延伸
collections的defaultdict的妙用
python内置的defaultdict为数据统计提供了绝好的接口!参加上面蒙特卡罗策略评估代码,我们需要统计一系列状态的价值,只需要声明:
returns_sum = defaultdict(float)
returns_count = defaultdict(float)
python被作为大多数人的数据统计工具,绝非浪得虚名。
enumerate的一般使用方法
循环迭代一个列表(集合)时,往往需要同时获得迭代的索引和元素,enumerate正是为此而生:
for i,x in enumerate(episode) if x[0] == state
上面的代码中,i即为迭代的索引,x为迭代到的元素,一箭双雕。
matplotlib的花花衣裳
matplotlib支持若干的style,上面蒙特卡罗方法进行策略评估给出的图形是ggplot风格的。下面的代码可以列出matplotlib支持的所有风格:
print(matplotlib.pyplot.style.available)
