Example 3.5-grid world
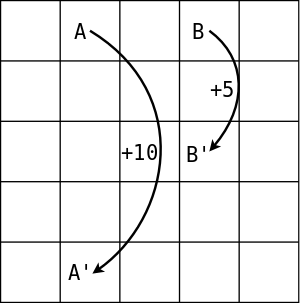
下图是一个grid world,每个格子代表了一个状态,从每个格子出发可以有4个动作:up/left/down/right,每个动作机会均等,如果动作的结果超出了边界,则格子的状态保持不变,并且获得的奖励为-1;从A格子出发的任何动作都会导致状态转移到A’格子,并且获得奖励+10;从B格子出发的任何动作都会导致状态转移到B’格子,并且获得奖励+5;其他任何情况的奖励为0。假设\(\gamma=0.9\),试计算每个格子的状态价值函数。
解析
这是一个典型的MDP问题,有限的状态空间,有限的动作空间。但是,我们面临两个棘手的问题:
- 根据Bellman等式,当前状态的价值依赖于下一个状态的价值,这是一个递归的过程。从何处开始,在何处结束?对于每一个状态都有不同的episode。
- 状态空间和动作空间如何表达?状态空间的表达容易想到使用格子的坐标来表示,比如格子A的状态可表示为坐标(0,1),那么动作空间如何表达比较合适呢?
Bellman等式的迭代求解
根据bellman求解MDP问题一般有两种思路:第一,如果MDP的状态转移矩阵是已知的,则可以精确的数值求解:求解线性方程组而已 ,参见价值函数以及其中的例子。第二,Bellman等式本身是一个迭代公式,因此可以通过迭代的方式逐步逼近状态价值函数。这种方式对状态转移矩阵不敏感,即无论是否知道状态转移矩阵都可以使用,也非常适合于编程实现。
迭代求解状态价值函数的基本步骤为:
-
初始化状态价值矩阵,一般初始化为0。这是计算的起点,此时每个状态的价值函数都是0。
-
根据Bellman等式,计算每个状态的新的价值函数。注意这一步不是一个递归的过程,因为上一轮的状态价值矩阵是已知的,在这一轮直接可以根据上一轮的状态价值矩阵计算新的价值函数即可,即:
\[v_{k+1}(s)=\sum_a \pi(a\mid s)\sum_{r,s'}p(s',r\mid s,a)\left[r+\gamma v_k(s')\right]\tag{1}\]其中的\(k\)代表了迭代的轮次(episode),注意不要和每个轮次(episode)中的时刻(步骤)的\(t\)混淆了。
-
计算每个轮次迭代的误差,达到设定的误差范围即可停止迭代,此时即获得了最终的状态价值函数。
这种迭代求解状态价值函数的方法称为”Policy Evaluation(Prediction)”,即对于任意给定的策略\(\pi\),都可以通过迭代的方式逐步逼近求解状态价值函数。但是,必须确保这种迭代求解的方法对于任意策略\(\pi\)都是收敛的,证明如下:
仔细观察式1,并对照Bellman等式(式2):
\[v_{\pi}(s)=\sum_a \pi(a\mid s)\sum_{r,s'}p(s',r\mid s,a)\left[r+\gamma v_{\pi}(s')\right]\tag{2}\]可以看出,式1只是对式2的简单变量替换,由\(v_{\pi}\)替换为\(v_k\),而式2在\(\gamma < 1\)或者episode能够在有限步内结束时即收敛(在回报一节中有证明),因此式1在同样的条件下也会收敛,即迭代求解状态价值函数的方法的收敛条件为:或者\(\gamma < 1\),或者所解决的MDP问题的episode是有限的。这两个条件几乎总是能够满足其中之一的。
动作空间的表示方式
动作对状态的影响表现为状态坐标的改变,因此将动作定义为对状态坐标的偏移量是个合理的方案,这样可以直接将状态和动作相加即可获得“下一个状态”。以动作up为例,其对状态的影响为横坐标不变,纵坐标增加+1,因此可以将up定义为[0,1]。同理,动作down可以定义为[0,-1]。
程序实现
有了上面的分析,下面的程序实现就不难理解了:
#######################################################################
# Copyright (C) #
# 2019 Baochen Su(subaochen@126.com) #
# 2016-2018 Shangtong Zhang(zhangshangtong.cpp@gmail.com) #
# 2016 Kenta Shimada(hyperkentakun@gmail.com) #
# Permission given to modify the code as long as you keep this #
# declaration at the top #
#######################################################################
import numpy as np
WORLD_SIZE = 5
A_POS = [0, 1]
A_PRIME_POS = [4, 1]
B_POS = [0, 3]
B_PRIME_POS = [2, 3]
DISCOUNT = 0.9
# 把动作定义为对x,y坐标的增减改变
ACTIONS = [np.array([0, -1]), # up
np.array([-1, 0]), # left
np.array([0, 1]), # down
np.array([1, 0])] # right
ACTION_PROB = 0.25
def step(state, action):
"""每次走一步
:param state:当前状态,坐标的list,比如[1,1]
:param action:当前采取的动作,是对状态坐标的修正
:return:下一个状态(坐标的list)和reward
"""
if state == A_POS:
return A_PRIME_POS, 10
if state == B_POS:
return B_PRIME_POS, 5
next_state = (np.array(state) + action).tolist()
x, y = next_state
if x < 0 or x >= WORLD_SIZE or y < 0 or y >= WORLD_SIZE:
reward = -1.0
next_state = state
else:
reward = 0
return next_state, reward
def grid_world_value_function():
"""计算每个单元格的状态价值函数
"""
# 状态价值函数的初值
value = np.zeros((WORLD_SIZE, WORLD_SIZE))
episode = 0
while True:
episode = episode + 1
# 每一轮迭代都会产生一个new_value,直到new_value和value很接近即收敛为止
new_value = np.zeros_like(value)
for i in range(WORLD_SIZE):
for j in range(WORLD_SIZE):
for action in ACTIONS:
(next_i, next_j), reward = step([i, j], action)
# bellman equation
# 由于每个方向只有一个reward和s'的组合,这里的p(s',r|s,a)=1
new_value[i, j] += ACTION_PROB * (reward + DISCOUNT * value[next_i, next_j])
error = np.sum(np.abs(new_value - value))
if error < 1e-4:
break
# 观察每一轮次状态价值函数及其误差的变化情况
print(f"{episode}-{np.round(error,decimals=5)}:\n{np.round(new_value,decimals=2)}")
value = new_value
if __name__ == '__main__':
grid_world_value_function()
完整源码请参见:grid world源码
结果解读
上面程序的计算结果如下图所示:
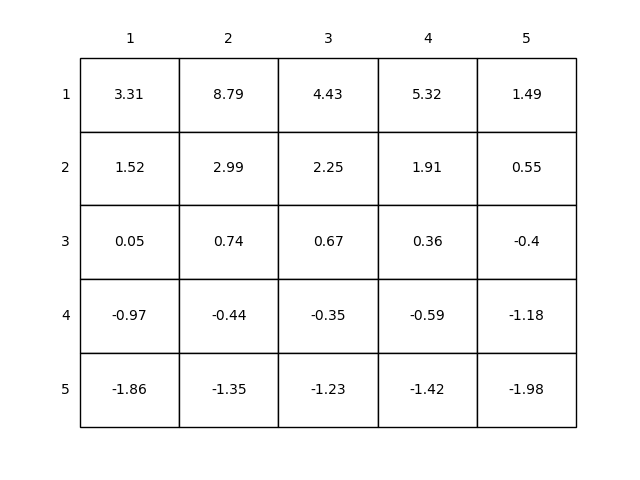
可以看出,靠近下边的格子,尤其是靠近边界的格子的状态价值偏小,这是因为靠近边界的格子很容易出界,而出界的奖励是-1;格子A的价值最高,这是很容易理解的,因为从A到A’的奖励是+10。但是为什么格子A的价值<10呢?这是因为从A到A’的奖励尽管是+10,但是A’的价值却是负值,导致A的价值会跟着损失一些。格子B的价值分析方法类似。
