最优策略（optimal policy）

面对一个问题，可能有策略千万条，哪一条是最好的呢？事实上，总是存在：

如果策略$\pi$使得其状态的回报（return）的期望大于或者等于其他任意的策略$\pi^{'}$，则称策略$\pi$为最优策略。

状态的回报的期望即为$v_{\pi}(s)$，即：$$\mathbb{E}_{\pi}[G_t

S_t=s,A_t=a]$。也就是说，对于任意状态$s\in\mathcal{S}$都有$v_{\pi}(s)>=v_{\pi^{‘}}(s)$，则称$v_{\pi}(s)$为最优状态价值函数，记为$v_*(s)$$。显然有：

\[v_*(s)=\max_{\pi}v_{\pi}(s), \forall s\in\mathcal{S}\]

如下图所示，对于给定的状态s，存在不同的策略$\pi$，使得从状态s到动作a的路径不同。不同的路径回报不同，能够使得状态s的回报最大的策略$\pi$即为最优策略，记为$\pi_*$。

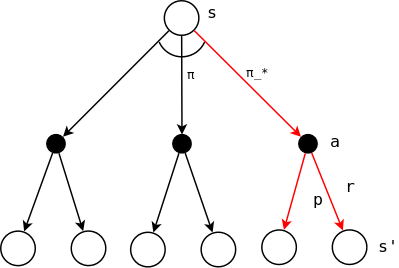
optimal-policy-value-function

直观的理解，不同的动作方向会导向不同的状态$s'$，带来不同的状态价值（$s'$状态价值的加权平均，即期望）。能够使得$s'$的状态价值最大化的动作记为最优的动作，或者说是最优策略。也就是说，通过状态价值函数判断最优策略，需要计算下一级节点的状态价值的期望，这就是作者所说的“one-step search”，只需要往前走一步，即可以判断当前的动作组合中，哪个是最优的：能够使得$s'$的状态价值函数的期望最大化的动作，选择这个最优的动作即为最佳策略。显然，这是一种完全的“贪心算法”，只基于下一步做出的决策。幸运的是，$s'$的状态价值函数实际上已经包含了长期的价值（思考一下状态价值函数的定义），因此：

A one-step-ahead search yields the long-term optimal actions.

同理，对于最优动作价值函数$q(s,a)$也有类似的定义：

\[q_{*}(s,a)=\max_{\pi}q_{\pi}(s,a)\]

如果已知$q_*(s,a)$，此时的动作$a$已经是最优动作了，因此动作$a$导向的状态$s'$必然是最优的状态，求解$q_*(s,a)$只需要将动作$a$下的$s'$的价值加权平均即可：

\[\begin{align} q_*(s,a) &=\mathbb{E}[G_t\mid S_t=s,A_t=a]\\ &=\mathbb{E}[R_{t+1}+\gamma v_*(S_{t+1})\mid S_t=s,A_t=a]\tag{2} \end{align}\]

注意和通常的$q(s,a)$定义的区别：

\[\begin{align} q(s,a) &=\mathbb{E}[G_t\mid S_t=s, A_t=a]\\ &=\mathbb{E}[R_{t+1}+\gamma v(S_{t+1})\mid S_t=s,A_t=a] \end{align}\]

下图可以直观的解释$q_*(s,a)$的意义：

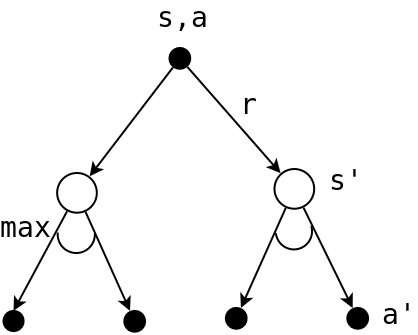
q-optimal-function

上面反复说的，其实是一个事情：

寻找最优策略，其实是寻找最优动作的过程：如何选取动作$a$，能够使得$q_*(s,a)$最大化$，此时的$q_*(s,a)$$即为最优的状态价值函数。

\[\begin{align} v_*(s) &=\max_{\pi}v_{\pi}(s)\\\tag{1.1} &=\max_a q_*(s,a)\\\tag{1.2} &=\max_a\mathbb{E}_{\pi_*}[G_t\mid S_t=s,A_t=a]\\\tag{1.3} &=\max_a\mathbb{E}_{\pi_*}[R_{t+1}+\gamma G_{t+1}\mid S_t=s,A_t=a]\\\tag{1.4} &=\max_a\mathbb{E}[R_{t+1}+\gamma v_*(S_{t+1})\mid S_t=a,A_t=a]\\\tag{1.5} &=\max_a\sum_{r,s'}p(s',r\mid s,a)[r+\gamma v_*(s')]\\\tag{1.6} \end{align}\]

上式每一个步骤的解释：

1.1，最佳状态函数的原始定义；
1.2，通常的状态价值函数是$q(s,a)$的加权平均，但是在寻找最佳状态函数的过程是找到一个动作$a$，使得$q(s,a)$最大化，最优的状态价值函数即为这个最大化的$q_*(s,a)$；
1.3，在最优策略$\pi_*$下$q_*(s,a)$的加权平均定义；
1.4，进一步的展开为immediaterly reward和长期回报，依然依赖于最优策略；
1.5，根据式2对$q_*(s,a)$的展开，此时已经不依赖于最优策略，但是其实$v_*$还是暗示了这是最优策略下的最优状态价值函数；
1.6，最终的最优状态价值函数的展开式，表达了当前时刻的最优价值函数和下一时刻的最优价值函数的关系，即Bellman最优等式

最优策略的案例：grid world问题

理论分析总是枯燥的，实战中寻找最优策略往往直接了当：对于每一个节点（时刻），计算动作空间产生的所有状态价值函数，选取最大的状态价值函数作为当前节点的状态价值，如此迭代循环，直到找到最优策略为止。

grid world问题参见：在那里，仅仅给出了在每个格子的状态价值函数（策略$\pi$为随机平均策略）。下面的方法可以计算grid world的最优策略：

def grid_world_optimal_policy():
    """计算格子世界的最优价值函数和最优策略
    """
    value = np.zeros((WORLD_SIZE, WORLD_SIZE))
    # 通过一个数组来表示每一个格子的最优动作，1表示在相应的方向上最优的
    optimal_policy = np.zeros((WORLD_SIZE, WORLD_SIZE, len(ACTIONS)))
    episode = 0
    while True:
        episode = episode + 1
        # keep iteration until convergence
        new_value = np.zeros_like(value)
        for i in range(WORLD_SIZE):
            for j in range(WORLD_SIZE):
                # 保存当前格子所有action下的state value
                action_values = []
                for action in ACTIONS:
                    (next_i, next_j), reward = step([i, j], action)
                    # value iteration
                    action_values.append(reward + DISCOUNT * value[next_i, next_j])
                new_value[i, j] = np.max(action_values)
                optimal_policy[i, j] = get_optimal_actions(action_values)
        error = np.sum(np.abs(new_value - value))
        if error < 1e-4:
            break
        # 观察每一轮次状态价值函数及其误差的变化情况
        print(f"{episode}-{np.round(error,decimals=5)}:\n{np.round(new_value,decimals=2)}")
        value = new_value
    print(f"optimal policy:{optimal_policy}")


def get_optimal_actions(values):
    """计算当前轮次格子的最优动作
    :param values:格子的状态价值
    :return: 当前的最优动作。解读这个最优动作数组，要参考ACTIONS中四个动作的方向定义，
    数值为1表示此动作为最优动作
    """
    optimal_actions = np.zeros(len(ACTIONS))
    indices = np.where(values == np.amax(values))
    for index in indices[0]:
        optimal_actions[index] = 1
    return optimal_actions

grid world的最优价值函数如下图所示：

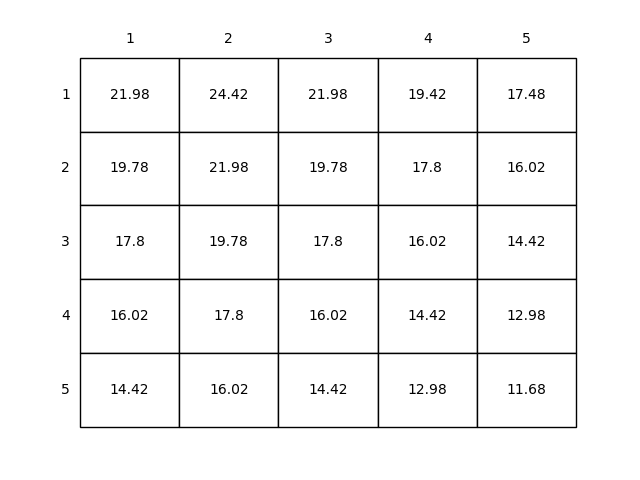
figure 3.5

完整的grid world程序参见：grid world源码