Ex 3.22:
Consider the continuing MDP shown as below. The only decision to be made is that in the top state, where two actions are available, left and right. The numbers show the rewards that are received deterministically after each action. There are exactly two deterministic policies, \(\pi_{left}\) and \(\pi_{right}\). What policy is optimal if \(\gamma=0\)? If \(\gamma=0.9\)? If \(\gamma=0.5\)?
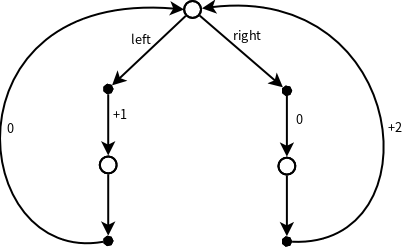
解答:
分别计算两个动作left和right下的状态价值函数:
\[\begin{align} v_{\pi_{left}}&=1+\gamma(0+\gamma v_{\pi_{left}})\\ v_{\pi_{right}}&=0+\gamma(2+\gamma v_{\pi_{right}}) \end{align}\]很容易得出:
\[\begin{align} v_{\pi_{left}}&=\frac{1}{1-\gamma^2}\\ v_{\pi_{right}}&=\frac{2\gamma}{1-\gamma^2} \end{align}\]即,当\(\gamma<0.5\)时,\(v_{\pi_{left}} > v_{\pi_{right}}\),反之\(v_{\pi_{left}} < v_{\pi_{right}}\);当\(\gamma=0.5\)时,\(v_{\pi_{left}} = v_{\pi_{right}}\)。
根据最有价值函数的定义,当\(\gamma<0.5\)时,应该选择left动作作为最优策略;当\(\gamma>0.5\)时,应该选择right动作作为最优策略;当\(\gamma=0.5\)时,两个动作都是最优策略。
