对于Policy improvement作者没有给出严格的数学证明,其实至少从下面的角度可以严格证明Policy improvement的可行性。
从期望的一个性质说起
首先证明期望的一个性质:
至少存在一个随机变量\(x\),其值不小于随机变量\(X\)的期望\(\mathbb{E}[X]\)
证明如下:(参见《概率论基础教程》P251)
设\(f\)为定义在有限集\(A\)上的函数,假定我们对该函数的最大值感兴趣:
\[m = \max_{s\in\mathcal{A}}f(s)\]为得到\(m\)的下界,令\(S\)为取值于\(A\)的随机元,显然有:\(m\ge f(S)\),即:
\[\mathbb{E}[m]\ge\mathbb{E}[f(S)]\]即:
\[m\ge\mathbb{E}[f(S)]\]也就是说,函数\(f\)的最大值不小于\(f\)的期望,即在有限集\(A\)上,一定存在值(最大值)不小于\(f\)的期望。
状态价值函数和动作价值函数的关系
有了以上的结论,我们考察\(v_{\pi}(s)\)和\(q_{\pi}(s,a)\)的关系:
\[v_{\pi}(s)=\sum_{a}\pi(a\mid s)q_{\pi}(s,a)\]即在策略\(\pi\)下,状态\(s\)的价值\(v_{\pi}(s)\)为\(q_{\pi}(s,a)\)的期望,因此一定存在至少一个\(q_{\pi}(s,a)\)的最大值使得\(q_{\pi}(s,a)\ge v_{\pi}(s)\)。亦即,在动作\(A\)的集合中,一定存在至少一个动作\(a\),其\(q(s,a)\)不小于状态\(s\)的价值\(v(s)\)。此结论对于任意\(s\in\mathcal{S}\)都成立。
我们定义对于任意\(s\in\mathcal{S}\)使得\(q_{\pi}(s,a)\)取最大值的策略为\(\pi^{'}\),其动作为\(a'\),即:
\[a'=\pi^{'}(s)\]于是有:
\[q_{\pi}(s,\pi^{'}(s))\ge v_{\pi}(s),\forall s\in\mathcal{S}\label{eq1}\tag{1}\]policy improvement可行性证明
利用上面的结论(公式\(\ref{eq1}\)),我们可以证明: \(v_{\pi^{'}}(s)\ge v_{\pi}(s),\forall s\in\mathcal{S}\)
即greedy policy是policy improvement的可行策略。
证明如下: \(\begin{align} v_{\pi}(s)&\le q_{\pi}(s,\pi^{'}(s))\tag{2-1}\\ &=\mathbb{E}[R_{t+1}+\gamma v_{\pi}(S_{t+1})\mid S_t=s,A_t=\pi^{'}(s)]\tag{2-2}\\ &=\mathbb{E}_{\pi^{'}}[R_{t+1}+\gamma v_{\pi}(S_{t+1})\mid S_t=s]\tag{2-3}\\ &\le\mathbb{E}_{\pi^{'}}[R_{t+1}+\gamma q_{\pi}(S_{t+1},\pi^{'}(S_{t+1}))\mid S_t=s]\tag{2-4}\\ &=\mathbb{E}_{\pi^{'}}[R_{t+1}+\gamma\mathbb{E}_{\pi^{'}}[R_{t+2}+\gamma v_{\pi}(S_{t+2})\mid S_{t+1},A_{t+1}=\pi^{'}(S_{t+1})]\mid S_t=s]\tag{2-5}\\ &=\mathbb{E}_{\pi^{'}}[R_{t+1}+\gamma R_{t+2}+\gamma^2v_{\pi}(S_{t+2})\mid S_t=s] \tag{2-6}\\ &=\mathbb{E}_{\pi^{'}}[R_{t+1}+\gamma R_{t+2}+\gamma^2R_{t+3}+\gamma^3v_{\pi}(S_{t+3})\mid S_t=s]\tag{2-7}\\ &\vdots\tag{2-8}\\ &\le\mathbb{E}_{\pi^{'}}[R_{t+1}+\gamma R_{t+2}+\gamma^2R_{t+3}+\gamma^3R_{t+4}+\ldots\mid S_t=s]\tag{2-9}\\ &=v_{\pi^{'}}(s)\tag{2-10} \end{align}\)
上面的证明中,值得注意以下步骤:
-
2-2是\(q_{\pi}(s,\pi^{'}(s))\)的展开。
-
2-3是2-2的等价变化,意为在策略\(\pi^{'}\)下的条件期望。进行这样的变换是为了方便后面推导出\(v_{\pi^{'}}(s)\),因为状态价值函数是\(v_{\pi^{'}}(s)\)以状态\(S_t\)为条件对策略\(\pi^{'}\)的期望。
-
2-4根据公式\(\ref{eq1}\)将\(v_{\pi}\)替换为\(q_{\pi}\)。
-
2-5是\(q_{\pi}(S_{t+1},\pi^{'}(S_{t+1}))\)的展开。
-
2-6是使用了期望的加法规则和“期望的期望是其本身”这个期望的性质,有必要单独拿出来说一下。
具体来说,2-6的推导过程可参见下图:
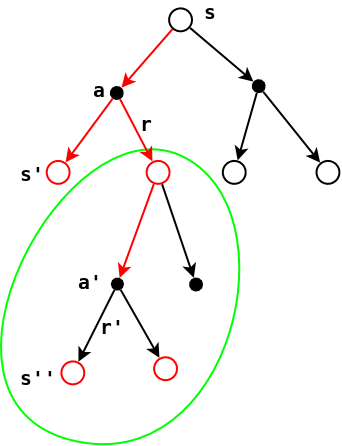
其中:
- 3-2和3-3使用了期望的加法规则。
- 3-4脱去了\(A_{t+1}\)这个条件,因为在策略\(\pi^{'}\)下,总是会寻找最优的动作\(a\),这和期望的下标\(\pi^{'}\)有同样的含义,因此可以去掉这个条件。
- 3-5进一步脱掉了\(S_{t+1}\)这个条件。从上图可以看出,在策略\(\pi^{'}\)(寻找最优的动作\(a\))下求\(v_{\pi}(S_{t+2})\),无论从\(s\)出发还是从\(s'\)出发都是一样的,因此条件期望可以进一步简化掉多余的条件\(S_{t+1}\),其结果不会受到影响。
- 3-6将结果合并在一起,利用了期望的期望是其本身的性质。
也就是说,对于任意的\(s\in\mathcal{S}\),我们总是能够找到一个策略\(\pi^{'}\)使得其状态价值函数不小于策略\(\pi\)下的状态价值函数,即策略\(\pi^{'}\ge\pi\),这就是policy improvement的理论依据,具体的实现就是greedy策略:对于任意的\(s\in\mathcal{S}\),找到使\(q(s,a)\)最大化的动作\(a\)即为最优策略。
