动作价值函数Q是model-free问题的入口
在策略迭代中使用蒙特卡洛方法和DP中的思路一样,都是策略评估和策略增强两个过程交替进行,互相促进,最终收敛到最优策略。在策略评估过程中,我们可以使用状态价值函数\(v_{\pi}(s)\),正如MC学习笔记-蒙特卡罗方法进行状态价值评估中对blackjack的策略评估所示。
在策略增强中,如果model是已知的,则状态价值函数是很有用的,因此此时只要往前看一步,就可以计算出哪个动作能够获得最大的价值,那么这个动作就是策略增强这一步应该采取的动作。但是,如果model不可知(即model-free问题),则状态价值函数不可得,我们就必须设法计算动作的价值,然后选择最大价值的动作进行策略增强。
事实上,即便在model已知的情形下,如果能够直接计算动作的价值,也应该采取动作价值来进行策略增强:更加直接。
策略增强:采用greedy policy
在DP中,我们已经证明greedy policy在策略迭代中的有效性。在蒙特卡洛方法中,greedy policy同样有效。
首先,对于任意的\(s \in \mathcal{S}\),根据greedy policy的定义有:
\[\pi(s) = \underset{a}{\operatorname{argmax}}q(s,a)\]也就是说,从任意状态s出发,我们选择使得\(q(s,a)\)最大的动作a作为策略增强的方向。\(\pi(s)\)即为在策略\(\pi\)下从状态s出发的动作a,这是一个确定的值,即greedy policy下此概率为1。
其次,我们考察在策略迭代中的两个策略\(\pi_k\)及其后续策略\(\pi_{k+1}\)(greedy policy),对于任意状态\(s \in \mathcal{S}\)都有:
\[\begin{align} q_{\pi_{k}}(s,\pi_{k+1}(s)) & =q_{\pi_{k}}(s,\underset{a}{\operatorname{argmax}}q_{\pi_k}(s,a)) \\ &=\max_aq_{\pi_k}(s,a) \\ &\ge q_{\pi_k}(s,\pi_k(s)) \end{align}\]这就证明了greedy policy的收敛性。
下面是蒙特卡洛方法(Exploring Starts)的算法描述:

greedy policy寻找blackjack最优策略
代码参见:蒙特卡洛算法实现21点游戏的最佳策略
分别经过500000,1000000,2000000,5000000个episode后,greedy policy依然没有找到最优策略,比如经过500000个episode后的状态为:
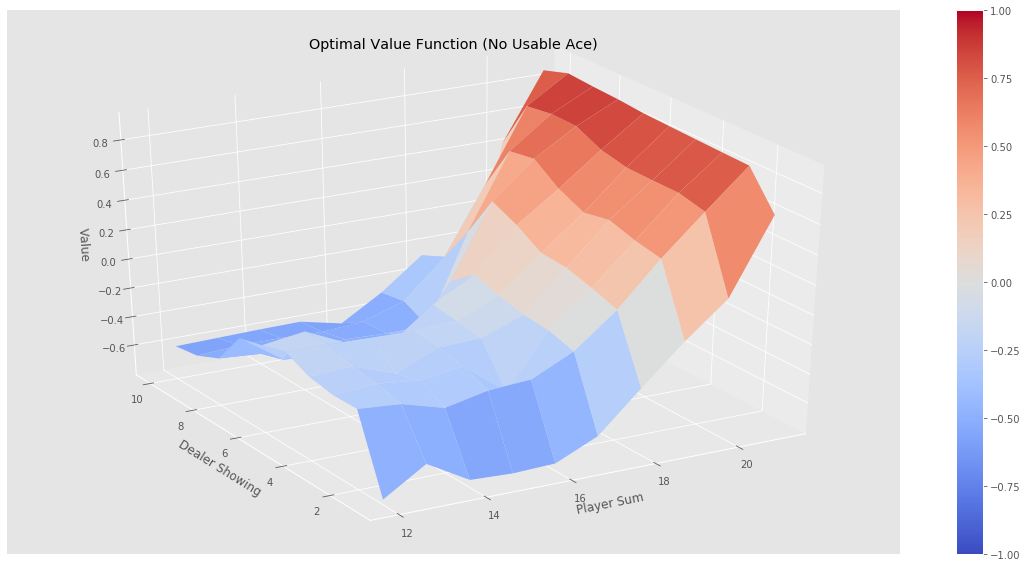
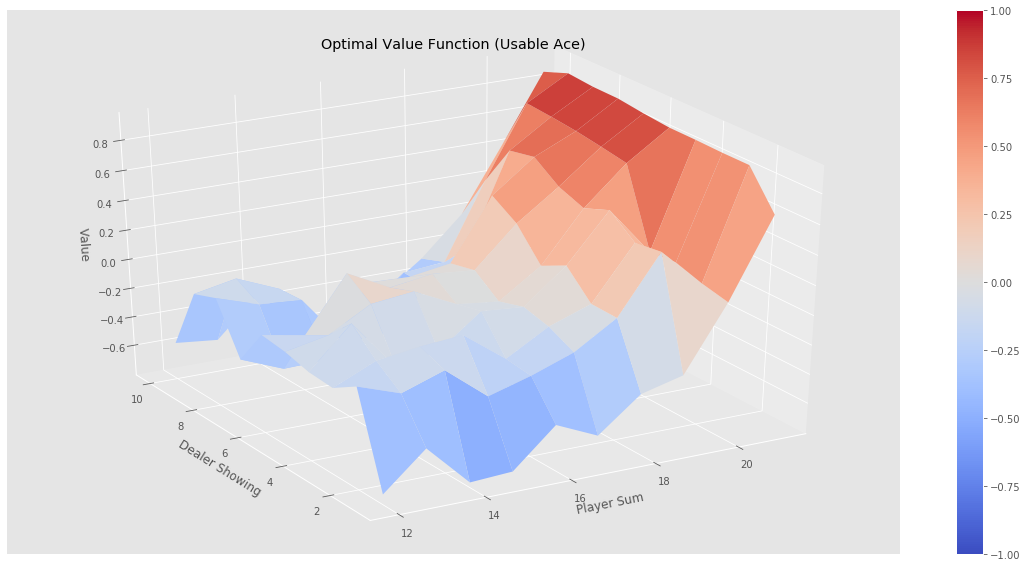
相应的,其策略图为:
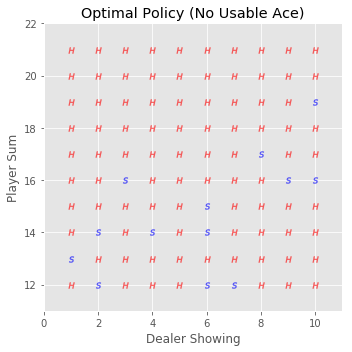
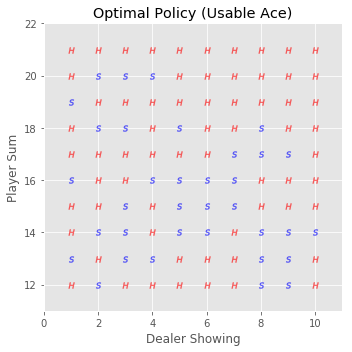
猜测,greedy policy没有找到blackjack的最优策略的原因可能有以下几个:
- 环境的代码有问题?如果环境没有给出随机的迭代起点状态,会导致greedy policy无法遍历所有的状态,即所谓的Exploring Starts问题。
- greedy policy非常强势,可能会导致最终能够访问到的状态有限,比如著名的“二道门”问题。
实际上,蒙特卡洛方法的两个基本限制就是:
- 是否能够遍历所有的<a,s>对?
- 是否能够在有限个episode内找到最优策略?
sutton的书中给出了greedy policy的最优策略,但是实验代码无法复现。只有通过下面阐述的\(\epsilon\)-greedy policy才能逼近sutton书中给出的最优策略,目前还不知道是哪里出了问题?
\(\epsilon\)-greedy policy
greedy policy非常强势,比如在david siliver的教程中给出了著名的“二道门”问题,会导致greedy policy形成一定的偏好,无法遍历所有的<a,s>对。
\(\epsilon\)-greedy policy的核心思想是在状态s选择动作的时候,不完全按照greedy policy的策略来进行,具体来说,假设动作空间的大小是m,则设置一个小的值\(\epsilon\),当选择动作的时候,有\(\epsilon/m\)的概率随机选择一个动作,有\(1-\epsilon\)的概率选择价值最大的动作,这样的策略就叫做\(\epsilon\)-greedy policy。
\(\epsilon\)-greedy policy以很小的概率随机选择动作,很好的解决了纯greedy policy的偏好问题,只要给出足够多的episode,即能够遍历所有的<a,s>对。
假设\(\pi^{'}\)为\(\epsilon\)-greedy policy,则其收敛性证明如下:
\[\begin{align} q_{\pi}(s,\pi^{'}(s))&=\sum_a\pi^{'}(a|s)q_{\pi}(s,a)\tag{2.1}\\ &=\frac{\epsilon}{|\mathcal{A}(s)|}\sum_aq_{\pi}(s,a)+(1-\epsilon)\underset{a}{\operatorname{max}}q_{\pi}(s,a)\tag{2.2}\\ &\ge\frac{\epsilon}{|\mathcal{A}(s)|}\sum_aq_{\pi}(s,a)+(1-\epsilon)\sum_a\frac{\pi(a|s)-\frac{\epsilon}{|\mathcal{A}(s)|}}{1-\epsilon}q_{\pi}(s,a)\tag{2.3}\\ &=\frac{\epsilon}{|\mathcal{A}(s)|}\sum_aq_{\pi}(s,a)+\sum_a\pi(a|s)q_{\pi}(s,a)-\frac{\epsilon}{|\mathcal{A}(s)|}\sum_aq_{\pi}(a,s)\tag{2.4}\\ &=\sum_a\pi(a|s)q_{\pi}(s,a)\\ &=v_{\pi}(s) & \end{align}\]| 式2.1只是一个分解:\(\epsilon\)-greedy policy将greedy policy的一个确定性的\(q(s,a)\)分解成了两个部分:greedy部分的概率是\(1-\epsilon\),其余部分的概率是$$\epsilon/ | \mathcal{A}(s) | $$。 |
式2.3是基于如下的事实:Q的最大值不小于其某种概率组合(可参见:policy improvement的数学证明)。需要进一步说明的是,恰好
\[\sum_a\frac{\pi(a|s)-\frac{\epsilon}{|\mathcal{A}(s)|}}{1-\epsilon}=1\]| 即,$$\sum_a\frac{\pi(a | s)-\frac{\epsilon}{ | \mathcal{A}(s) | }}{1-\epsilon}q_{\pi}(s,a)\(是\)q_{\pi}(s,a)$$的概率组合。 |
证明如下:
\[\begin{align} &\sum_a\frac{\pi(a|s)-\frac{\epsilon}{|\mathcal{A}(s)|}}{1-\epsilon}\\ &=\frac{1}{1-\epsilon}\sum_a\left(\pi(a|s)-\frac{\epsilon}{|\mathcal{A}(s)|}\right)\\ &=\frac{1}{1-\epsilon}\left(\sum_a\pi(a|s)-\sum_a\frac{\epsilon}{|\mathcal{A}(s)|}\right)\\ &=\frac{1}{1-\epsilon}(1-\epsilon)\\ &=1 \end{align}\]上式基于如下的事实:
-
$$\sum_a\pi(a s)=1$$,这是显然的,从状态s出发的所有动作a的概率之和为1。 -
$$\sum_a\frac{\epsilon}{ \mathcal{A}(s) }=\epsilon\(,这是因为每一个非greedy policy动作的概率为\)\frac{\epsilon}{ \mathcal{A}(s) }\(,则所有的非greedy policy动作概率之和恰好为\)\epsilon$$。
\(\epsilon\)-greedy policy的算法描述如下:

\(\epsilon\)-greedy policy寻找blackjack最优策略
代码参见:epsilon greedy policy寻找blackjack最有策略的代码实现
最终的状态图如下:
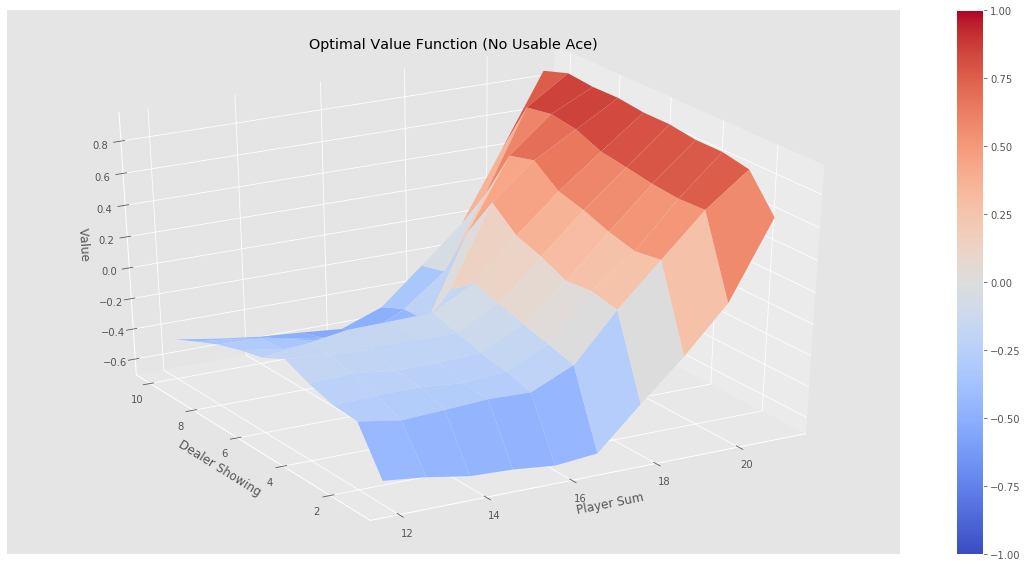
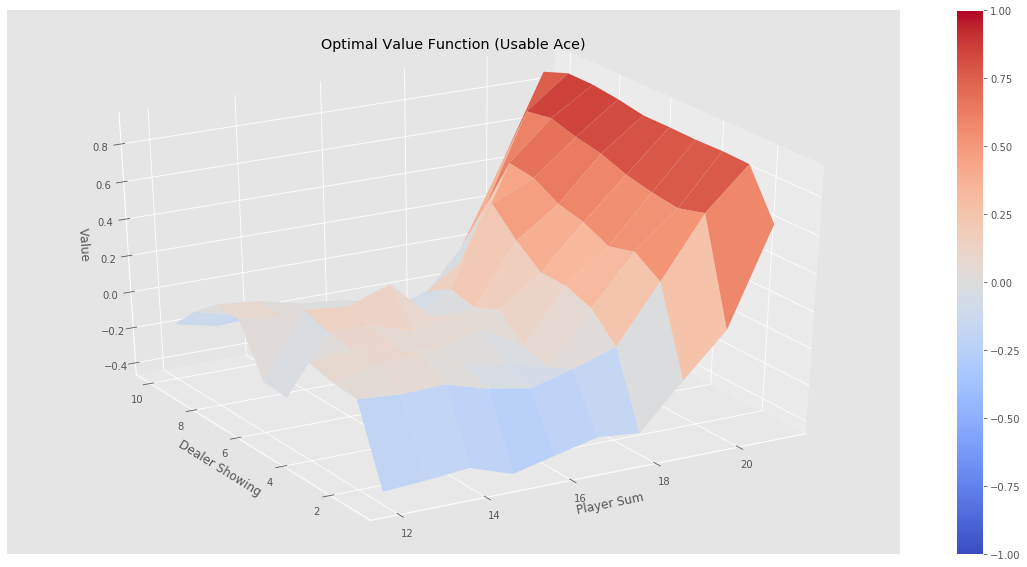
最终的策略图如下(H表示Hit动作,S表示Stick动作):
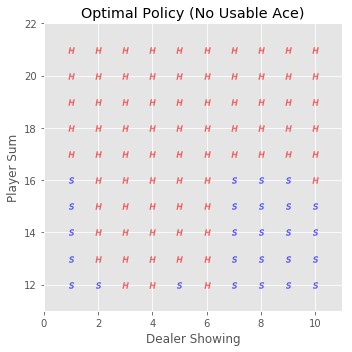
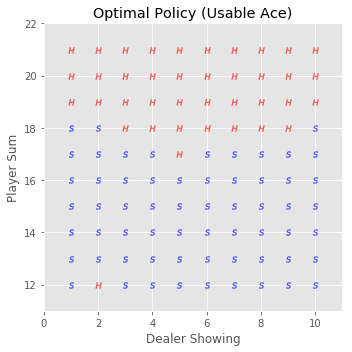
可见,\(\epsilon\)-greedy policy所找到的最优策略要比单纯的greedy policy好的多。
