关于Exercise 3.11的解析

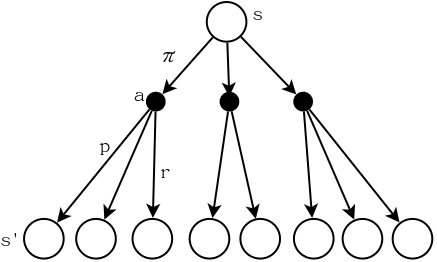
Exercise 3.11：

If the current state is $S_t$, and actions are selected according to stochastic policy $\pi$, then what is the expectation of $R_{t+1}$ in term of $\pi$ and the four-argument function $p$ (3.2)?

解析如下：

这个问题涉及到两个重要的（概念）概率：

策略$\pi$，表示在状态$s$下采取动作$a$的概率，记做$\pi(a\mid s)$。
状态转移概率$p$，表示在状态$s$下采取动作$a$时，到达状态$s'$并且奖励为$r$的概率，记做$p(s',r\mid s,a)$。

所求为$$\mathbb{E}{\pi}[R{t+1}

S_t=s]$，即在状态$S_t$下，采取策略$\pi$时$R_{t+1}$的期望。由于$\pi$是一个随机策略，因此动作$a$在这里也是一个变量，其概率分布为$\pi(a\mid s)$。为了简化问题，我们首先假设动作$a$不变。叠加状态$S_t$已知这个条件，即状态$s$和动作$a$都已知的情况下，$R_{t+1}$$的期望可以表示为：

\[\mathbb{E}_{\pi}[R_{t+1}|S_t=s]=\sum_{r\in\mathcal{R}}r\sum_{s'\in\mathcal{S}}p(s',r\mid s,a)=\sum_{r,s'}rp(s',r\mid s,a)\tag{1}\]

这个式子其实就是$r(s,a)$，即在$s,a$都是已知（固定）的前提下奖励的期望。

但是在这里$a$不是固定的，而是遵守策略$\pi$或者说符合概率分布$\pi(a\mid s)$，因此上面式1的计算还需要叠加策略$\pi$的影响。也就是说，式1是在$a$固定时得出的，则当$a$也是一个变量时，存在多个动作$a$，需要将每一个动作$a$都考虑进去（即$\sum\pi(a\mid s)=1$）：

\[\mathbb{E}_{\pi}[R_{t+1}|S_t=s]=\sum_{a\in\mathcal{A}}\pi(a\mid s)\sum_{r\in\mathcal{R}}r\sum_{s'\in\mathcal{S}}p(s',r\mid s,a)=\sum_{a,r,s'}\pi(a\mid s)rp(s',r\mid s,a)\tag{2}\]

在式2中，只有$s$是已知的，$a,s',r$都是变量。从下面的图可以直观的理解这个式子的意义：