奖励和回报

强化学习的目标是最大化Rewards。这里的Rewards不仅仅包括immediately reward，也包括后续时刻（步骤）的一系列reward。通常使用Return（回报）\(G_t\)来表示Rewards的累积结果：

\[G_t = R_{t+1}+\gamma R_{t+2}+\gamma^2R_{t+3}+\ldots=\sum_{k=0}^{\infty}\gamma^{k}R_{t+k+1}\]

其中，\(\gamma\in [0,1]\)的衰减因子，表示对长期reward的权重。

于是，强化学习的目标变成最大化Return（回报）。

\(G_t\)可以表示为迭代的形式（递推公式）：

\[\begin{align} G_t&=R_{t+1}+\gamma R_{t+2}+\gamma^2R_{t+3}+\gamma^3R_{t+4}+\ldots\\ &=R_{t+1}+\gamma(R_{t+2}+\gamma R_{t+3}+\gamma^2R_{t+4}+\ldots)\\ &=R_{t+1}+\gamma G_{t+1} \end{align}\]

有两点需要特别注意：

\(G_t\)表示Agent在t时刻的Return（回报）。也就是说，从t时刻开始一直到episode结束（即T时刻，或者到达终止状态的时刻）所经历的每一个时刻（步骤）的reward的累加。在episode的每一个时刻都可以计算相应的回报\(G_t\)。
所谓的immediately reward（即时回报），可以理解为往前走一步所得到的回报，即\(R_{t+1}\)。试想，如果Agent站在t时刻不动，它就不知道会得到多少奖励，只有勇敢的往前迈出一步，才能收到Environment给出的反馈（reward和下一个状态，关于状态的影响后面再谈，这里只谈reward）。所以，将t时刻的回报定义为从t+1时刻的奖励\(R_{t+1}\)开始计算是合理的。

策略函数

从时刻t（状态为s）到时刻T（终止状态），根据策略的不同，Agent实际上可能存在多种路径，即在时刻t（状态s），根据不同的策略，可以选择不同的动作\(a\)。 策略函数\(\pi(a\mid s)\)是指Agent在状态s下选取动作a的概率，因此\(\pi(a\mid s)\)是一个2元的概率函数，表示从状态s到动作a的映射概率。

\(\pi(a\mid s)\)是强化学习中需要优化的参数之一：在迭代优化过程中，需要不断调整\(\pi(a\mid s)\)使得最终的结果胜率最高。

状态价值函数和动作价值函数

前面说过，从t时刻到T时刻，不同的策略会导致不同的探索路径，如下图所示：

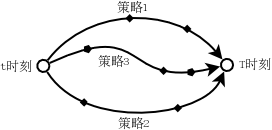
policy

如果我们站在t时刻思考，采取什么策略到达T时刻是最优的策略？那么必须有办法衡量在t时刻（状态为s）不同策略下的价值，即能够获得的累积奖励，这就是状态价值函数的由来：\(v_{\pi}(s)\)表达了状态s在策略\(\pi\)下的好坏（状态价值函数），可以使用return的期望来衡量：

\[v_{\pi}(s)=\mathbb{E_{\pi}}[G_t\mid S_t=s]=\mathbb{E_{\pi}}\left[\sum_{k=0}^{\infty}\gamma^kR_{t+k+1}|S_t=s\right]\]

如下面的backup diagram所示：

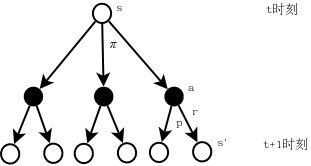
value-function-backup-diagram

假设当前处于状态s，即\(S_t=s\)。在策略\(\pi\)的作用下，从状态s可以有三个动作可以选择，每个动作进入Environment后会有2个后续状态s’及其对应的reward：r，于是当我们评价状态s的价值时，就需要将最后一层的所有reward进行加权平均（求期望），因为最后一层所有的reward都是状态s的可能结果。这是一个递归的过程，即最后一层的状态s’还会有相应的动作a’，接着是新的状态s’‘……

注意状态价值函数\(v_{\pi}(s)\)是一个关于回报的加权平均（期望），而回报是对奖励（reward）的（衰减）累加，因此状态价值函数本质上是对reward的计算。在状态价值函数的计算公式中，除了奖励r外，其他因子都是权重调整因子。

\(v_{\pi}(s)\)中的k表示计算第几层的return加权平均（通过student mdp的例子说明计算过程）

在实际的MDP计算中，也常引入\(q_{\pi}(s,a)\)，表示状态s在策略\(\pi\)下，采取动作a的好坏（动作价值函数）：

\[q_{\pi}(s,a)=\mathbb{E_{\pi}}[G_t\mid S_t=s,A_t=a]=\mathbb{E_{\pi}}\left[\sum_{k=0}^{\infty}\gamma^kR_{t+k+1}|S_t=s,A_t=a\right]\]

下图有助于理解\(q_{\pi}(s,a)\)，见图中橙色线条标出部分。

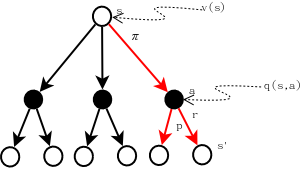
q-function-backup-diagram

从上图可以看出，\(q_{\pi}(s,a)\)实际上是由两部分构成的：

immediaterly reward，即\(r\)。注意到从动作\(a\)到状态\(s'\)并非只有一个固定的\(r\)值，比如reward服从某种随机分布的情形。比如，假设我们往前走一步所获得奖励\(r\)是一个随机数，该随机数从集合{1,2,3}按照分布列{20%,20%,60%}获得。
状态\(s'\)的回报的加权平均（期望），即\(\mathbb E_{\pi}[G_{t+1}\mid S_{t+1}=s']\)，即\(v_{\pi}(s')\)。考虑到衰减因子\(\gamma\)，这一项为\(\gamma v_{\pi}(s')\)。这里之所以使用状态\(s'\)的回报的期望，是因为从动作\(a\)出发可能存在多个状态\(s'\)，因此需要将每个状态\(s'\)的回报考虑进来进行加权平均计算。

另外还需要注意到，每一个奖励\(r\)和一个状态转移概率（dynamic function）对应，即\(p(s',r\mid s,a)\)，表示从动作\(a\)到状态\(s'\)获得奖励\(r\)的概率为\(p\)。因此，从动作\(a\)到状态\(s'\)，如果不考虑权重，其总的reward累积为：

\[r+\gamma \mathbb{E}[G_{t+1}|S_{t+1}=s']=r+\gamma v_{\pi}(s')\]

由此，\(q_{\pi}(s,a)\)可以展开为下式：

\[\begin{align} q_{\pi}(s,a) &=\sum_{r}\sum_{s'}p(s',r\mid s,a)[r+\gamma\mathbb{E_{\pi}}[G_{t+1}\mid S_{t+1}=s']\\ &=\sum_{r,s'}p(s',r\mid s,a)[r+\gamma v_{\pi}(s')]\tag{1} \end{align}\]

上式中，\(\sum_{r}\sum_{s'}p(s',r\mid s,a)\)可以这样理解：从动作\(a\)到状态\(s'\)可能存在多个路径，即存在多个\(s'\)。先固定（计算）一个\(s'\)计算\(q_{\pi}(s,a)\)，则需要考虑每一个reward的情形（每一个可能的reward对应一个\(p\)，对于每一个reward有\(\sum p=1\)）。如此计算每一个\(s'\)，就是\(\sum_r\sum_{s'}\)了，参见下图，这是其中一个\(s'\)的计算路径：\(p1(r1+\gamma v_{\pi}(s'))+p2(r2+\gamma v_{\pi}(s'))+p3(r3+\gamma v_{\pi}(s')),其中p1+p2+p3=1\)

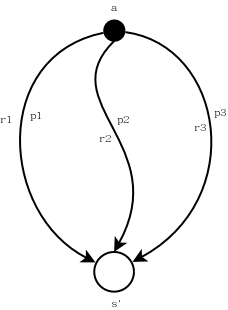
注意到，\(q_{\pi}(s,a)\)也是一个关于reward的加权平均，相对于\(v_{\pi}(s)\)而言，\(q_{\pi}(s,a)\)的计算起点是从动作\(a\)开始的，而\(v_{\pi}(s)\)是从状态\(s\)开始的，因此\(q_{\pi}(s,a)\)是\(v_{\pi}(s)\)的一个组成部分，后面我们会获得\(q_{\pi}(s,a)\)和\(v_{\pi}(s)\)的关系式，可以清楚的看到这一点。

从上图也可以看出\(q_{\pi}\)和\(v_{\pi}\)的关系：

\[v_{\pi}(s)=\sum_{a}\pi(a\mid s)q_{\pi}(s,a)\]

将\(q_{\pi}(s,a)\)的展开式代入可得：

\[v_{\pi}(s)=\sum_{a}\pi(a\mid s)\sum_{r,s'}p(s',r\mid a,s)[r+\gamma v_{\pi}(s')]\]

这就是著名的状态价值函数的Bellman等式，即迭代公式。

从正面推导一下Bellman等式： \(\begin{align} v_{\pi}(s)&=\mathbb{E}_{\pi}[R_{t+1}+\gamma G_{t+1}\mid S_t=s]\\ &=\mathbb{E}_{\pi}[R_{t+1}\mid S_t=s]+\mathbb{E}_{\pi}[\gamma G_{t+1}\mid S_t=s]\\ &=\sum_{a}\pi(a\mid s)\sum_r r\sum_{s'}p(s',r\mid s,a)\\&\quad+\gamma\sum_a\pi(a\mid s)\sum_r \sum_{s'}p(s',r\mid s,a)\mathbb{E}_{\pi}[ G_{t+1}\mid S_{t+1}=s']\\ &=\sum_{a}\pi(a\mid s)\sum_r \sum_{s'}rp(s',r\mid s,a)\\&\quad+\gamma\sum_a\pi(a\mid s)\sum_r \sum_{s'}p(s',r\mid s,a)\mathbb{E}_{\pi}[ G_{t+1}\mid S_{t+1}=s']\\ &=\sum_{a}\pi(a\mid s)\sum_{r,s'}rp(s',r\mid s,a)\\&\quad+\gamma\sum_a\pi(a\mid s)\sum_{r,s'}p(s',r\mid s,a)\mathbb{E}_{\pi}[ G_{t+1}\mid S_{t+1}=s']\\ &=\sum_a\pi(a\mid s)\sum_{r,s'}p(s',r\mid s,a)\left[r+\gamma v_{\pi}(s')\right] \end{align}\)

上面的推导过程用到了Exersice 3.11的结论，参见：关于Exercise 3.11的解析。需要注意的是，条件\(S_t=s\)是如何过渡到\(S_{t+1}=s'\)的：从状态\(s\)到\(s'\)经过了两个路径。我在很长时间里面没有搞清楚这个条件是如何变化的，直到有一天突然开了窍。

作者在这里有一段非常精彩的论述，摘录如下：

where it is implicit that the actions, \(a\), are taken from the set \(\mathcal A(s)\), that the next states, \(s'\) , are taken from the set \(\mathcal{S}\) (or from \(\mathcal{S}+\) in the case of an episodic problem), and thatt he rewards, \(r\), are taken from the set \(\mathcal{R}\). Note also how in the last equation we havem erged the two sums, one over all the values of \(s'\) and the other over all the values of \(r\), into one sum over all the possible values of both. We use this kind of merged sum often to simplify formulas. Note how the final expression can be read easily as an expected value. It is really a sum over all values of the three variables, \(a\), \(s'\) , and \(r\). For each triple, we compute its probability, \(\pi(a\mid s)p(s' , r \mid s, a)\), weight the quantity in brackets by that probability, then sum over all possibilities to get an expected value.

案例分析

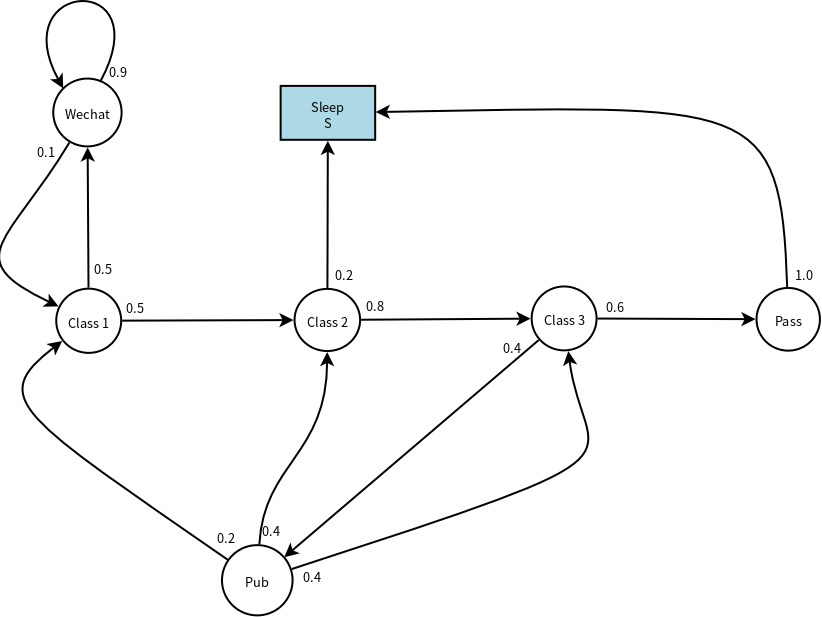
下面是一个有趣的例子（替换了原作中的Facebook为Wechat），其中的圆圈代表了“状态”，方框代表了“结束状态”，每条线段（弧线）标明了状态转移的方向和概率。假设这门课只需要三节课就可结业，那么下图表达了同学们在学习过程中的各种状态及其转移概率。比如，上第一节课的时候，你有50%的概率顺利进入了第二节课，但是也有50%的概率经受不住微信的诱惑开始不停的刷。而刷微信容易上瘾，即90%的情况下你会不停的刷，直到某个时刻（10%的概率）重新回到第一节课。在第三节课，可能有40%的概率觉得差不多了，就到Pub喝点小酒庆祝……

当然，这个例子的状态图并没有完整描述上课的所有状态序列，这只是其中的一种可能状态序列。

注意到，每个状态节点的出线概率之和一定为1。比如，第二节课有两条出线，一条指向S节点（概率为0.2），一条指向C3节点（概率为0.8）。这很容易理解：有几条出线代表了从当前状态存在几种转移到其他状态的路径。

makov-chains-student-1

由此，概率转移矩阵为（矩阵的列顺序为C1C2C3PpassPubWechatSleep，如果能够标出矩阵行和列的label能够更清楚的说明问题，可惜在markdown里面不知道如何操作）：

\[P=\left[\begin{matrix} &0.5&&&&0.5&\\ &&0.8&&&&0.2\\ &&&0.6&0.4&&\\ &&&&&&1.0\\ 0.2&0.4&0.4&&&&\\ 0.1&&&&&0.9&\\ &&&&&& \end{matrix}\right]\]

于是，下面的采样序列都是合理的，也可以计算这样的采样序列的达成概率。

C1-C2-C3-Pass-Sleep：非常认真的学生
C1-Wechat-Wechat-C1-C2-Sleep：第一节课走神的学生
C1-C2-C3-Pub-C1-Wechat-Wechat-Wechat-C1-C2-C3-Pub-C3-Pass-Sleep：经常走神的学生

下面给状态转移图加上reward，即每个状态的immediately reward，参见下图：

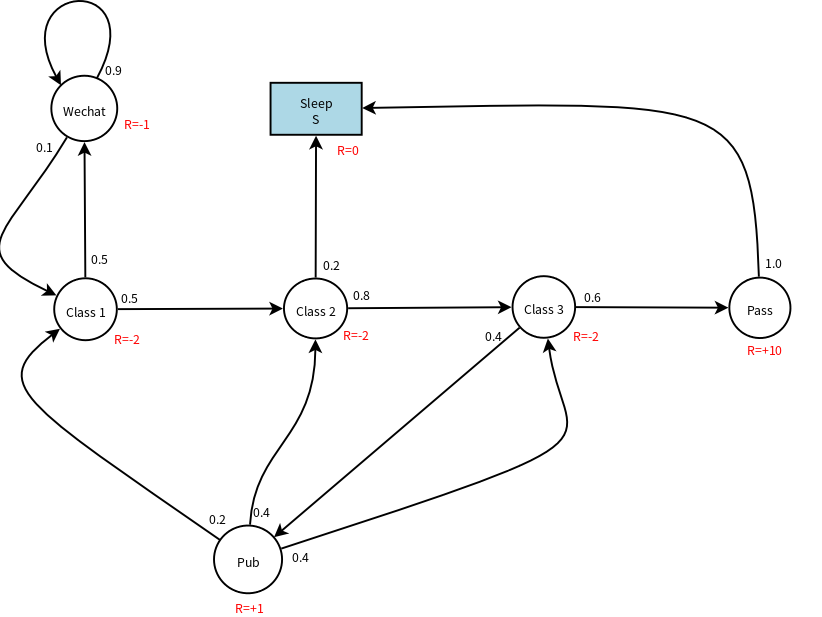
student-mdp-reward

下面以\(\gamma=1\)为例，计算节点C3的价值，如下图所示，节点C3的价值和C3的即时奖励以及下一节点的价值有关（根据状态价值函数的递推公式）。显然，Pass节点的价值为10，因为从Pass节点只有一条出线，其immediaterly reward=10。

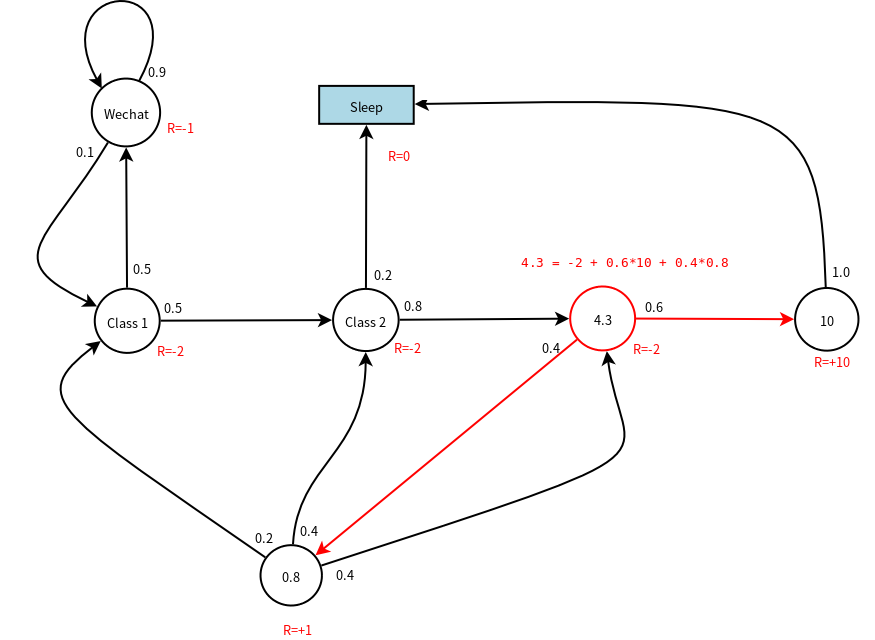
student-mdp-reward-c3

上图中，计算C3节点的价值时使用到了Pub节点的价值，那么Pub节点的价值0.8是如何计算出来的呢？实际上，假设C1，C2，C3，Pass，Pub，Wechat，Sleep节点的价值分别为v1,v2,v3,v4,v5,v6,v7，我们可以列出如下的方程：

\[\begin{align} v1&=-2+\gamma(0.5*v2+0.5*v6)\\ v2&=-2+\gamma(0.8*v3+0.2*v7)\\ v3&=-2+\gamma(0.6*v4+0.4*v5)\\ v4&=10+\gamma(1.0*v7)\\ v5&=1+\gamma(0.2*v1+0.4*v2+0.4*v3)\\ v6&=-1+\gamma(0.1*v1+0.9*v6)\\ v7&=0 \end{align}\]

写成矩阵的形式为：

\[\left[\begin{matrix} v1\\v2\\v3\\v4\\v5\\v6\\v7 \end{matrix}\right]= \left[\begin{matrix} -2\\-2\\-2\\10\\1\\1\\0 \end{matrix}\right]+\gamma \left[\begin{matrix} &0.5&&&&0.5&\\ &&0.8&&&&0.2\\ &&&0.6&0.4&&\\ &&&&&&1.0\\ 0.2&0.4&0.4&&&&\\ 0.1&&&&&0.9&\\ &&&&&& \end{matrix}\right] \left[\begin{matrix} v1\\v2\\v3\\v4\\v5\\v6\\v7 \end{matrix}\right]\]

即：

\[\mathcal{v}=\mathcal{R}+\gamma\mathcal{P}\mathcal{v}\]

对于小规模MDP问题，可以直接矩阵求解：

\[\mathcal{v}=(1-\gamma\mathcal{P})^{-1}\mathcal{R}\]

结果如下图所示：

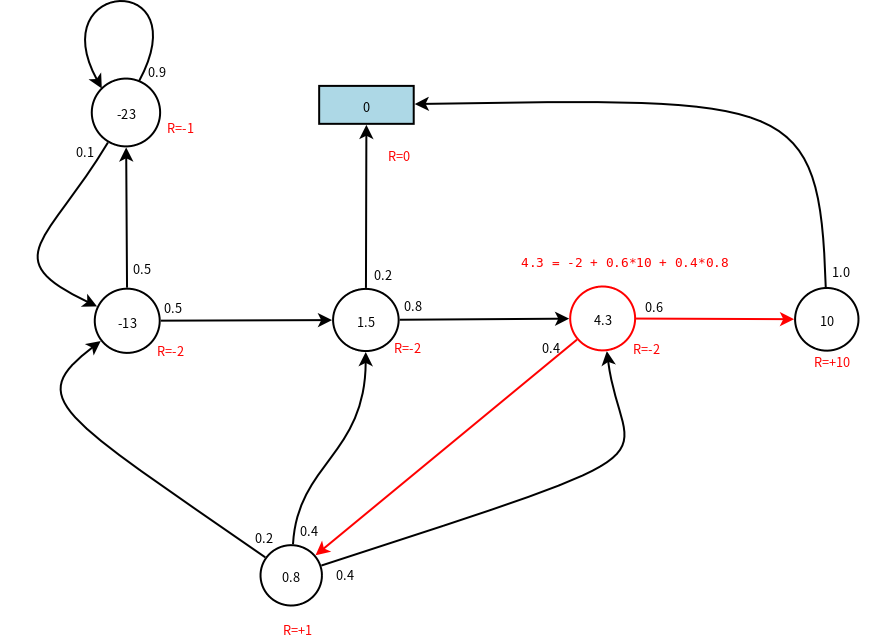
student-mdp-status-value

附：求解以上线性方程组的octave文件

gamma=1.0 # gamma
R=[-2;-2;-2;10;1;-1;0] # immediately reward
P=[0 0.5 0 0 0 0.5 0; # status transition matrix
0 0 0.8 0 0 0 0.2;
0 0 0 0.6 0.4 0 0;
0 0 0 0 0 0 1.0;
0.2 0.4 0.4 0 0 0 0;
0.1 0 0 0 0 0.9 0;
0 0 0 0 0 0 0]
V=inv(eye(7)-gamma*P)*R # status value